《理論》〈電気回路〉[H19:問9]RLC並列回路のインピーダンスの大小比較に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

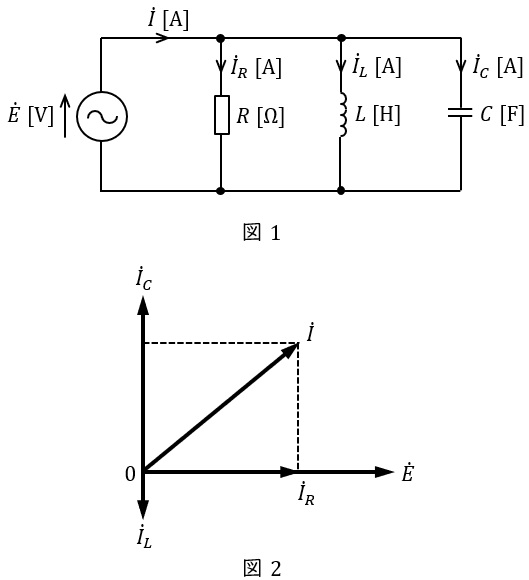
図1に示す，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサからなる並列回路がある。この回路に角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の交流電圧\( \ \dot E \ \mathrm {[V]} \ \)を加えたところ，この回路に流れる電流\( \ \dot I \ \mathrm {[A]} \ \)，\( \ {\dot I}_{R} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{L} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{C} \ \mathrm {[A]} \ \)のベクトル図が図2に示すようになった。このときの\( \ L \ \)と\( \ C \ \)の関係を表す式として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle \omega L ＜ \frac {1}{\omega C} \ \)　　(2)　\( \ \displaystyle \omega L ＞ \frac {1}{\omega C} \ \)　　(3)　\( \ \displaystyle \omega ^{2}=\frac {1}{\sqrt {LC}} \ \)　
　(4)　\( \ \displaystyle \omega L = \frac {1}{\omega C} \ \)　　(5)　\( \ \displaystyle R=\sqrt {\frac {L}{C}} \ \)

【ワンポイント解説】

\( \ RLC \ \)並列回路における電流の関係からインピーダンスの関係を考える問題です。
本問は図2のベクトル図に着目して解いていく問題で，すべての科目に関係する電験を合格する上では必須の内容です。さらに(3)と(4)はどちらも並列共振の条件で変形したら全く同じ式になるので，正答ではないと気付けると理想かと思います。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
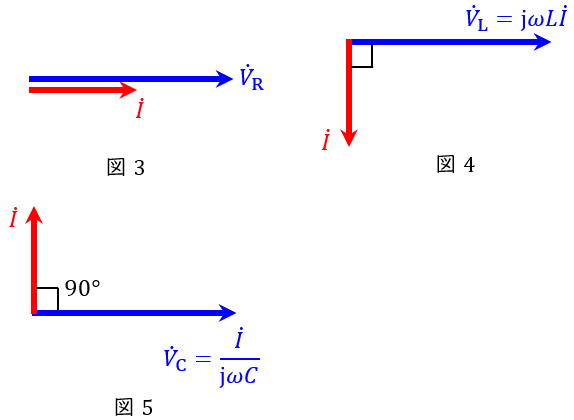
\] となります。この関係をベクトル図に表すと，図3～図5となります。

【解答】

解答：(2)
図2より，\( \ I_{C} ＞ I_{L} \ \)なので，ワンポイント解説「1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り，
\[
\begin{eqnarray}
I_{C}& \ ＞ \ & I_{L} \\[ 5pt ] \omega CE& \ ＞ \ & \frac {E}{\omega L} \\[ 5pt ] \omega C& \ ＞ \ & \frac {1}{\omega L} \\[ 5pt ] \omega L& \ ＞ \ &\frac {1}{\omega C}
\end{eqnarray}
\] と求められる。