《理論》〈電磁気〉[H25:問4]ループ状導体に働く力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

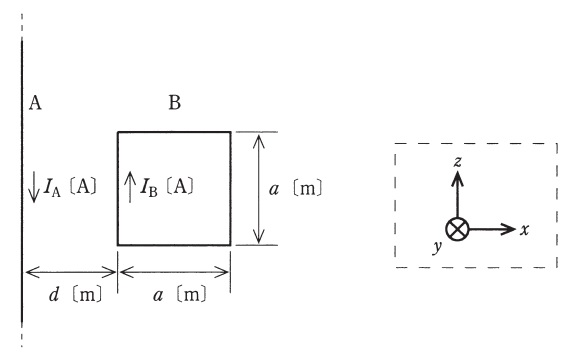
図のように，透磁率\( \ \mu _{0} \ \mathrm {[H/m]} \ \)の真空中に無限に長い直線状導体\( \ \mathrm {A} \ \)と\( \ 1 \ \)辺\( \ a \ \mathrm {[m]} \ \)の正方形のループ状導体\( \ \mathrm {B} \ \)が距離\( \ d \ \mathrm {[m]} \ \)を隔てて置かれている。\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)は\( \ xz \ \)平面上にあり，\( \ \mathrm {A} \ \)は\( \ z \ \)軸と平行，\( \ \mathrm {B} \ \)の各辺は\( \ x \ \)軸又は\( \ z \ \)軸と平行である。
\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)には直線電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)が，それぞれ図示する方向に流れている。このとき，\( \ \mathrm {B} \ \)に加わる電磁力として，正しいものを次の(1)～(5)のうちから一つ選べ。

なお，\( \ xyz \ \)座標の定義は，破線の枠内の図で示したとおりとする。

(1)　\( \ 0 \ \mathrm {[N]} \ \)　つまり電磁力は生じない

(2)　\( \ \displaystyle \frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a^{2}}{2\pi d\left( a+d\right) } \ \mathrm {[N]} \ \)の\( \ +x \ \)方向の力

(3)　\( \ \displaystyle \frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a^{2}}{2\pi d\left( a+d\right) } \ \mathrm {[N]} \ \)の\( \ -x \ \)方向の力

(4)　\( \ \displaystyle \frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a\left( a +2d\right) }{2\pi d\left( a+d\right) } \ \mathrm {[N]} \ \)の\( \ +x \ \)方向の力

(5)　\( \ \displaystyle \frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a\left( a +2d\right) }{2\pi d\left( a+d\right) } \ \mathrm {[N]} \ \)の\( \ -x \ \)方向の力

【ワンポイント解説】

問3と同じような知識を求められる問題です。本問で使用する電磁気の法則は非常に重要な内容となりますので，必ず理解するようにして下さい。

1.アンペアの周回積分の法則
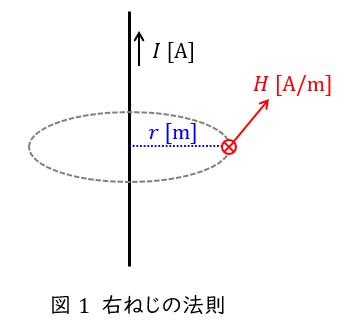
電流\( \ I \ \mathrm {[A]} \ \)の流れる向きに右ねじを合わせる(図1においては上向き)と，右ねじを回す向きに磁界\( \ H \ \mathrm {[A / m ]} \ \)が発生し，距離\( \ r \ \mathrm {[m]} \ \)離れた場所の磁界の大きさは，
\[
\begin{eqnarray}
H &=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

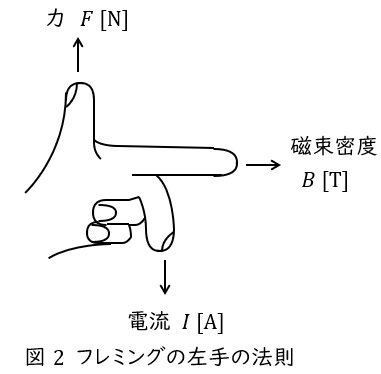
2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

3.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係
磁束密度\( \ B \ \mathrm {[T]} \ \)と磁界の大きさ\( \ H \ \mathrm {[A / m ]} \ \)には，透磁率を\( \ \mu \ \mathrm {[H / m ]} \ \)とすると，
\[
\begin{eqnarray}
B &=&\mu H \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(2)
右ねじの法則及びフレミングの左手の法則に沿って，導体\( \ \mathrm {B} \ \)の各辺に加わる磁界及び電磁力を図3に示す。ただし，横軸に加わる力は上辺と下辺で向きが逆で同じ大きさとなるため省略した。

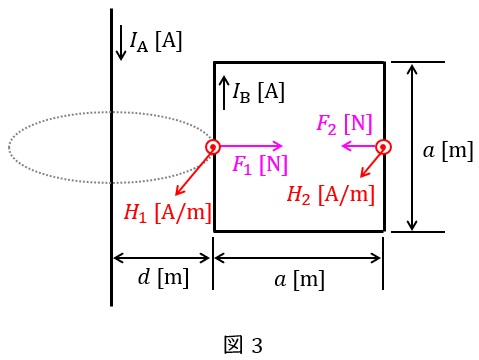
図3における各辺の磁界の大きさ\( \ H_{1} \ \mathrm {[A / m ]} \ \)及び\( \ H_{2} \ \mathrm {[A / m ]} \ \)は，ワンポイント解説「1.アンペアの周回積分の法則」より，
\[
\begin{eqnarray}
H_{1} &=&\frac {I_{\mathrm {A}}}{2\pi d} \\[ 5pt ] H_{2} &=&\frac {I_{\mathrm {A}}}{2\pi \left( a + d\right) } \\[ 5pt ] \end{eqnarray}
\] であり，それぞれの磁束密度の大きさ\( \ B_{1} \ \mathrm {[T]} \ \)及び\( \ B_{2} \ \mathrm {[T]} \ \)は，ワンポイント解説「3.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」より，
\[
\begin{eqnarray}
B_{1} &=&\mu _{0}H_{1} \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}}{2\pi d} \\[ 5pt ] B_{2} &=&\mu _{0}H_{2} \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}}{2\pi \left( a + d\right) } \\[ 5pt ] \end{eqnarray}
\] となる。したがって，各辺に加わる電磁力\( \ F_{1} \ \mathrm {[N]} \ \)及び\( \ F_{2} \ \mathrm {[N]} \ \)は，ワンポイント解説「2.フレミングの左手の法則」より，
\[
\begin{eqnarray}
F_{1} &=&B_{1}I_{\mathrm {B}}a \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi d} \\[ 5pt ] F_{2} &=&B_{2}I_{\mathrm {B}}a \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi \left( a + d\right) } \\[ 5pt ] \end{eqnarray}
\] となるので，導体\( \ \mathrm {B} \ \)に加わる合成の力\( \ F \ \mathrm {[N]} \ \)は，\( \ F_{1} \ \mathrm {[N]} \ \)及び\( \ F_{2} \ \mathrm {[N]} \ \)の向きに注意すると，
\[
\begin{eqnarray}
F &=&F_{1}-F_{2} \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi d}-\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi \left( a + d\right) } \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi } \left( \frac {1}{d}-\frac {1}{a+d}\right) \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi } \frac {\left( a+d\right) -d}{d\left( a + d\right) } \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a}{2\pi } \frac {a}{d\left( a + d\right) } \\[ 5pt ] &=&\frac {\mu _{0}I_{\mathrm {A}}I_{\mathrm {B}}a^{2}}{2\pi d\left( a + d\right) } \\[ 5pt ] \end{eqnarray}
\] と求められ，\( \ F_{1} ＞ F_{2} \ \)であるから，力の方向は\( \ +x \ \)方向となる。