Contents
【問題】
【難易度】★★★☆☆(普通)
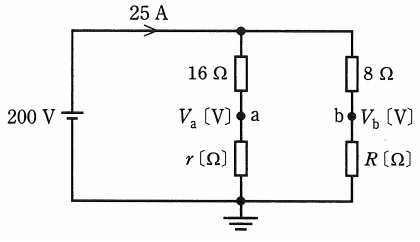
図の直流回路において,\( \ 200 \ \mathrm {[V]} \ \)の直流電源から流れ出る電流が\( \ 25 \ \mathrm {[A]} \ \)である。\( \ 16 \ \mathrm {[\Omega ]} \ \)と\( \ r \ \mathrm {[\Omega ]} \ \)の抵抗の接続点\( \ \mathrm {a} \ \)の電位を\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \),\( \ 8 \ \mathrm {[\Omega ]} \ \)と\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗の接続点\( \ \mathrm {b} \ \)の電位を\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)とする。\( \ V_{\mathrm {a}}=V_{\mathrm {b}} \ \)となる\( \ r \ \mathrm {[\Omega ]} \ \)と\( \ R \ \mathrm {[\Omega ]} \ \)の値の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& r & R \\
\hline
(1) & 2.9 & 5.8 \\
\hline
(2) & 4.0 & 8.0 \\
\hline
(3) & 5.8 & 2.9 \\
\hline
(4) & 8.0 & 4.0 \\
\hline
(5) & 8.0 & 16 \\
\hline
\end{array}
\]
【ワンポイント解説】
直流回路の回路計算に関する問題です。
電位が等しくなる条件と電圧と電流が成立する条件を使用して正答を導き出す必要があります。
基本公式を確実に理解しておくようにしましょう。
1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.分圧・分流の法則
①分圧の法則
図1に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]

②分流の法則
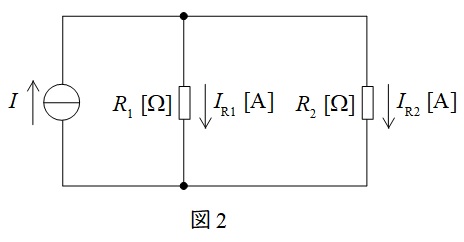
図2に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
【解答】
解答:(4)
点\( \ \mathrm {a} \ \)及び点\( \ \mathrm {b} \ \)の電位\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)及び\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)は,ワンポイント解説「2.分圧・分流の法則」より,
\[
\begin{eqnarray}
V_{\mathrm {a}}&=&\frac {r}{16+r}\times 200 \\[ 5pt ]
&=&\frac {200r}{16+r} \\[ 5pt ]
V_{\mathrm {b}}&=&\frac {R}{8+R}\times 200 \\[ 5pt ]
&=&\frac {200R}{8+R} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ V_{\mathrm {a}}=V_{\mathrm {b}} \ \)より,
\[
\begin{eqnarray}
\frac {200r}{16+r}&=&\frac {200R}{8+R} \\[ 5pt ]
\frac {r}{16+r}&=&\frac {R}{8+R} \\[ 5pt ]
r\left( 8+R\right) &=&R\left( 16+r\right) \\[ 5pt ]
8r+rR&=&16R+rR \\[ 5pt ]
8r&=&16R \\[ 5pt ]
r&=&2R \\[ 5pt ]
\end{eqnarray}
\]
となる。これを使用して,ワンポイント解説「1.合成抵抗」により回路の合成抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)を求めると,
\[
\begin{eqnarray}
R_{0}&=&\frac {\left( 16+2R\right) \left( 8+R\right) }{\left( 16+2R\right) +\left( 8+R\right) } \\[ 5pt ]
&=&\frac {2R^{2}+32R+128}{3R+24} \\[ 5pt ]
\end{eqnarray}
\]
となり,電源電圧が\( \ 200 \ \mathrm {[V]} \ \),流れ出る電流が\( \ 25 \ \mathrm {[A]} \ \)であるから,オームの法則より,
\[
\begin{eqnarray}
R_{0}&=&\frac {200}{25} \\[ 5pt ]
&=&8 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
8&=&\frac {2R^{2}+32R+128}{3R+24} \\[ 5pt ]
24R+192&=&2R^{2}+32R+128 \\[ 5pt ]
2R^{2}+8R-64&=&0 \\[ 5pt ]
R^{2}+4R-32&=&0 \\[ 5pt ]
\left( R+8\right) \left(R-4\right) &=&0 \\[ 5pt ]
R &=&4 \ \mathrm {[\Omega ]},-8 \ \mathrm {[\Omega ]}\left( 不適\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,
\[
\begin{eqnarray}
r&=&2R \\[ 5pt ]
&=&2\times 4 \\[ 5pt ]
&=&8 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは