Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のブリッジ回路を用いて,未知の抵抗の値\( \ R_{\mathrm {x}} \ \mathrm {[\Omega ]} \ \)を推定したい。可変抵抗\( \ R_{\mathrm {3}} \ \)を調整して,検流計に電流が流れない状態を探し,平衡条件を満足する\( \ R_{\mathrm {x}} \ \mathrm {[\Omega ]} \ \)の値を求める。求めた値が真値と異なる原因が,\( \ R_{k} \ \left( k=1,2,3\right) \ \)の真値からの誤差\( \ \Delta R_{k} \ \)のみである場合を考え,それらの誤差率\( \ \displaystyle \varepsilon _{k}=\frac {\Delta R_{k}}{R_{k}} \ \)が次の値であったとき,\( \ R_{\mathrm {x}} \ \)の誤差率として,最も近いものを次の(1)~(5)のうちから一つ選べ。
\( \ \displaystyle \varepsilon _{\mathrm {1}}=0.01 \ \), \( \ \displaystyle \varepsilon _{\mathrm {2}}=-0.01 \ \), \( \ \displaystyle \varepsilon _{\mathrm {3}}=0.02 \ \)
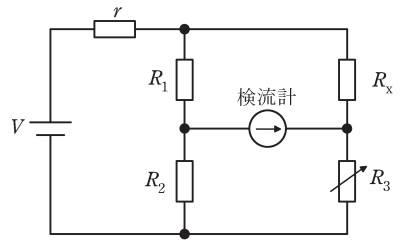
(1) \( \ 0.0001 \ \) (2) \( \ 0.01 \ \) (3) \( \ 0.02 \ \) (4) \( \ 0.03 \ \) (5) \( \ 0.04 \ \)
【ワンポイント解説】
各抵抗の誤差率から求める抵抗の総合誤差率を求める問題です。
少し数学的なテクニックを要する問題ですので,苦戦した受験生も多かったかもしれません。
1.誤差及び誤差率の定義
真値を\( \ T \ \),測定値を\( \ M \ \)とすると,誤差\( \ \varepsilon \ \)と誤差率\( \ %\varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ]
%\varepsilon &=&\frac {M-T}{T} \times 100 \ [%]
\end{eqnarray}
\]
となります。
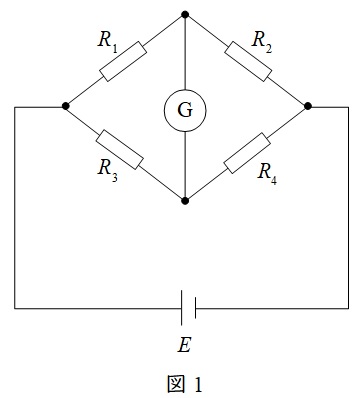
2.ブリッジの平衡条件
図1のようなブリッジ回路において,検流計に電流が流れないときの各抵抗の関係は,
\[
\begin{eqnarray}
R_{1}R_{4} &=&R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
もしくは,
\[
\begin{eqnarray}
\frac {R_{1}}{R_{3}} &=&\frac {R_{2}}{R_{4}} \\[ 5pt ]
\end{eqnarray}
\]
となります。(※覚えやすい方で覚えましょう)
【解答】
解答:(5)
ワンポイント解説「2.ブリッジの平衡条件」より,
\[
\begin{eqnarray}
R_{\mathrm {x}}R_{2}&=&R_{1}R_{3} \\[ 5pt ]
R_{\mathrm {x}}&=&\frac {R_{1}R_{3}}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ R_{\mathrm {1}} \ \),\( \ R_{\mathrm {2}} \ \),\( \ R_{\mathrm {3}} \ \)の誤差率\( \ \Delta R_{\mathrm {1}} \ \),\( \ \Delta R_{\mathrm {2}} \ \),\( \ \Delta R_{\mathrm {3}} \ \)が,
\[
\begin{eqnarray}
\Delta R_{\mathrm {1}}&=&\varepsilon _{\mathrm {1}}R_{\mathrm {1}} \\[ 5pt ]
&=&0.01R_{1} \\[ 5pt ]
\Delta R_{\mathrm {2}}&=&\varepsilon _{\mathrm {2}}R_{\mathrm {2}} \\[ 5pt ]
&=&-0.01R_{2} \\[ 5pt ]
\Delta R_{\mathrm {3}}&=&\varepsilon _{\mathrm {3}}R_{\mathrm {3}} \\[ 5pt ]
&=&0.02R_{3} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ R_{\mathrm {x}} \ \)の測定値\( \ R_{\mathrm {x}}+\Delta R_{\mathrm {x}} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {x}}+\Delta R_{\mathrm {x}}&=&\frac {\left( R_{\mathrm {1}}+\Delta R_{\mathrm {1}}\right) \left( R_{\mathrm {3}}+\Delta R_{\mathrm {3}}\right) }{\left( R_{\mathrm {2}}+\Delta R_{\mathrm {2}}\right) } \\[ 5pt ]
&=&\frac {\left( R_{\mathrm {1}}+0.01R_{1}\right) \left( R_{\mathrm {3}}+0.02R_{3}\right) }{\left( R_{\mathrm {2}}-0.01R_{2}\right) } \\[ 5pt ]
&=&\frac {1.01R_{1}\times 1.02R_{3}}{0.99R_{2}} \\[ 5pt ]
&≒&1.04\frac {R_{1}R_{3}}{R_{2}} \\[ 5pt ]
&=&1.04R_{\mathrm {x}} \\[ 5pt ]
&=&R_{\mathrm {x}}+0.04R_{\mathrm {x}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,誤差率は\( \ 0.04 \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは