Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のように,相電圧\( \ 200 \ \mathrm {V} \ \)の対称三相交流電源に,複素インピーダンス\( \ \dot Z =5\sqrt {3}+\mathrm {j}5 \ \mathrm {[\Omega ]} \ \)の負荷が\( \ \mathrm {Y} \ \)結線された平衡三相負荷を接続した回路がある。
次の(a)及び(b)の問に答えよ。
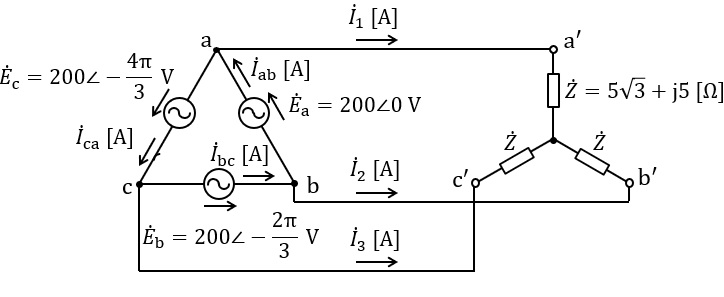
(a) 電流\( \ {\dot I}_{1} \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 20.00 \ ∠-\displaystyle \frac {\pi }{3} \ \) (2) \( \ 11.55 \ ∠-\displaystyle \frac {\pi }{3} \ \) (3) \( \ 16.51 \ ∠-\displaystyle \frac {\pi }{6} \ \)
(4) \( \ 20.00 \ ∠-\displaystyle \frac {\pi }{6} \ \) (5) \( \ 11.55 \ ∠-\displaystyle \frac {\pi }{6} \ \)
(b) 電流\( \ {\dot I}_{\mathrm {ab}} \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 20.00 \ ∠-\displaystyle \frac {\pi }{6} \ \) (2) \( \ 6.67 \ ∠-\displaystyle \frac {\pi }{6} \ \) (3) \( \ 11.55 \ ∠-\displaystyle \frac {\pi }{6} \ \)
(4) \( \ 6.67 \ ∠-\displaystyle \frac {\pi }{3} \ \ \ \) (5) \( \ 11.55 \ ∠-\displaystyle \frac {\pi }{3} \ \)
【ワンポイント解説】
\( \ \mathrm {\Delta } \ \)結線の電源と\( \ \mathrm {Y} \ \)結線の負荷を組み合わせた三相回路に関する問題です。
\( \ \mathrm {Y} \ \)結線の相電圧と線間電圧の関係,\( \ \mathrm {\Delta } \ \)結線の線電流と相電流の関係等を理解していることが求められる問題です。演習としてはとても良い問題と思います。
本問は平成24年問16からの再出題となります。
1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
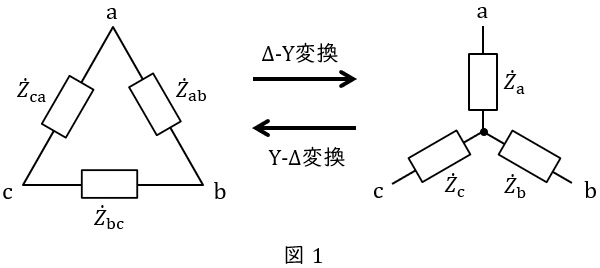
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\]
となります。
2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
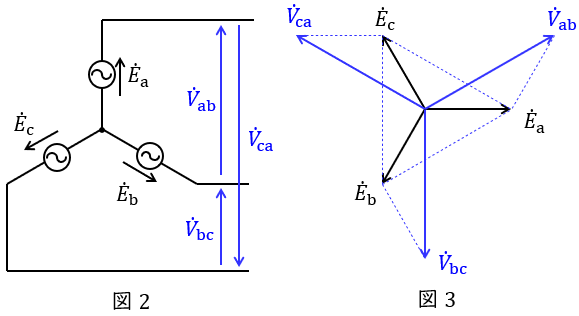
図2のような三相対称電源がある時,線間電圧と相電圧の関係は図3のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。
3.\( \ \Delta \ \)結線における相電流と線電流の関係
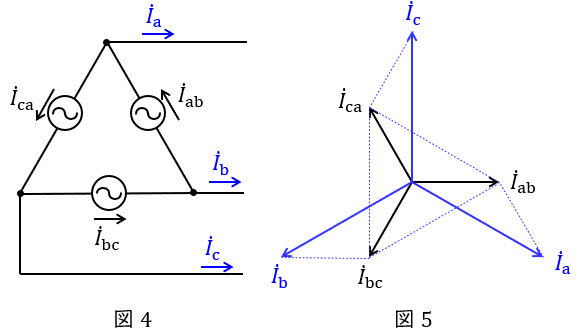
図4のような三相対称電源がある時,線電流と相電流の関係は図5のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
4.複素平面における複素数の表記方法
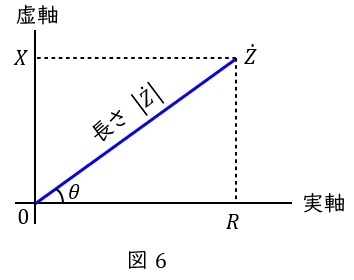
図6のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(2)
電源を\( \ \mathrm {Y} \ \)結線としたときの\( \ \mathrm {a} \ \)点の相電圧\( \ {E_{\mathrm {a}}}^{\prime } \ \mathrm {[V]} \ \)は,ワンポイント解説「2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,
\[
\begin{eqnarray}
{E_{\mathrm {a}}}^{\prime } &=&\frac {200}{\sqrt {3}}∠-\frac {\pi }{6} \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,複素インピーダンス\( \ \dot Z=5\sqrt {3}+\mathrm {j}5 \ \mathrm {[\Omega ]} \ \)を極座標表示にすると,ワンポイント解説「4.複素平面における複素数の表記方法」の通り,
\[
\begin{eqnarray}
\dot Z &=&\sqrt {\left( 5\sqrt {3}\right) ^{2}+5^{2}}∠\frac {\pi }{6} \\[ 5pt ]
&=&10∠\frac {\pi }{6} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{1} &=&\frac {{E_{\mathrm {a}}}^{\prime }}{\dot Z} \\[ 5pt ]
&=&\frac {\displaystyle \frac {200}{\sqrt {3}}∠-\frac {\pi }{6}}{\displaystyle 10∠\frac {\pi }{6}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {200}{\sqrt {3}}}{10} ∠ \left( -\frac {\pi }{6}-\frac {\pi }{6}\right) \\[ 5pt ]
&≒&11.55∠ -\frac {\pi }{3} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
(a)解答より,\( \ {\dot I}_{\mathrm {ab}} \ \mathrm {[A]} \ \)は,ワンポイント解説「3.\( \ \Delta \ \)結線における相電流と線電流の関係」の通り,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}} &=&\frac {11.55}{\sqrt {3}}∠ \left( -\frac {\pi }{3}+\frac {\pi }{6}\right) \\[ 5pt ]
&≒&6.67∠ -\frac {\pi }{6} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは