《理論》〈電磁気〉[R4上:問4]一様磁界中を動く直線導体に生じる誘導起電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

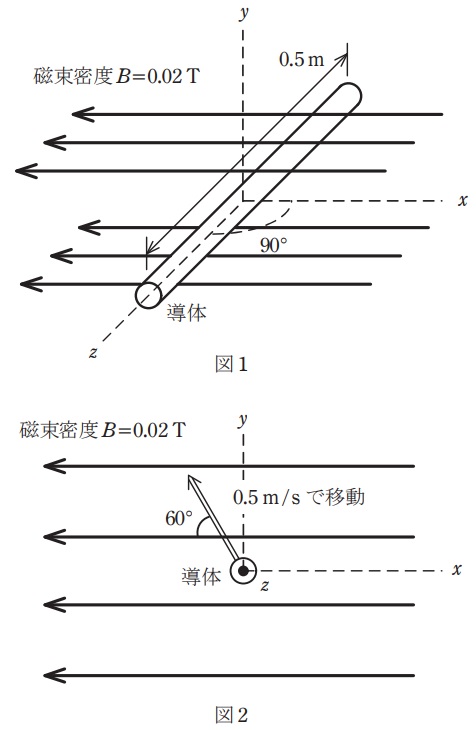
図1のように，磁束密度\( \ B＝0.02 \ \mathrm {T} \ \)の一様な磁界の中に長さ\( \ 0.5 \ \mathrm {m} \ \)の直線状導体が磁界の方向と直角に置かれている。図2のようにこの導体が磁界と直角を維持しつつ磁界に対して\( \ 60° \ \)の角度で，二重線の矢印の方向に\( \ 0.5 \ \mathrm {m / s} \ \)の速さで移動しているとき，導体に生じる誘導起電力\( \ e \ \)の値\( \ \mathrm {[mV]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，静止した座標系から見て，ローレンツ力による起電力が発生しているものとする。

　(1)　\( \ 2.5 \ \)　　(2)　\( \ 3.0 \ \)　　(3)　\( \ 4.3 \ \)　　(4)　\( \ 5.0 \ \)　　(5)　\( \ 8.6 \ \)　　

【ワンポイント解説】

一様磁界中の導体に生じる誘導起電力の大きさをフレミングの法則を用いて解く問題です。
本問のように斜めに動くような問題の場合，ほぼ確実に斜めに動かないパターンや\( \ \sin \ \)と\( \ \cos \ \)を間違えて計算したパターンの誤答があります。
斜めであることに忘れないようにできるだけ図に描いて，計算の中に取り込むようにして下さい。

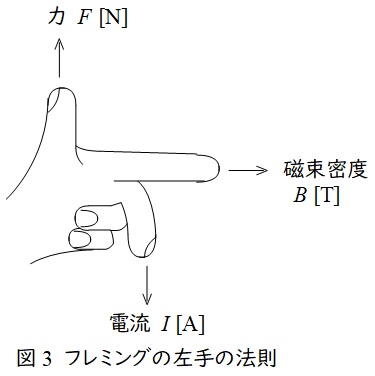
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

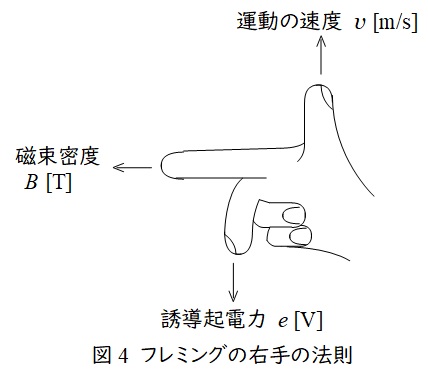
2.フレミングの右手の法則
親指を導体の運動方向，人差し指を磁界（磁束密度）の方向にすると，中指の方向に誘導起電力が発生するという法則で，磁束密度の大きさを\( \ B \ \mathrm {[T]} \ \)，導体の速度を\( \ v \ \mathrm {[m／s]} \ \)，導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，誘導起電力の大きさ\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
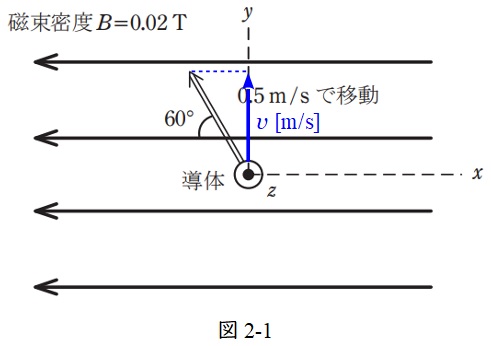
ワンポイント解説「2.フレミングの右手の法則」の通り，誘導起電力が発生するのは導体の運動方向と磁束密度の方向に対して直角の方向となるので，誘導起電力に影響する導体の運動方向は図2-1に示す成分である。
その速度の大きさを\( \ v \ \mathrm {[m / s]} \ \)とすると，
\[
\begin{eqnarray}
v &=& 0.5\sin 60° \\[ 5pt ] &=& 0.5\times \frac {\sqrt {3}}{2} \\[ 5pt ] &≒& 0.4330 \ \mathrm {[m / s]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，誘導起電力の大きさ\( \ e \ \mathrm {[mV]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] &=& 0.02\times 0.5\times 0.4330 \\[ 5pt ] &=& 0.00433 \ \mathrm {[V]}　→　4.3 \ \mathrm {[mV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。