《電力》〈変電〉[H23:問16]三相短絡事故発生時の事故電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

変電所に設置された一次電圧\( \ 66 \ \mathrm {[kV]} \ \)，二次電圧\( \ 22 \ \mathrm {[kV]} \ \)，容量\( \ 50 \ \mathrm {[MV\cdot A]} \ \)の三相変圧器に，\( \ 22 \ \mathrm {[kV]} \ \)の無負荷の線路が接続されている。その線路が，変電所から負荷側\( \ 500 \ \mathrm {[m]} \ \)の地点で三相短絡を生じた。

三相変圧器の結線は，一次側と二次側が\( \ \mathrm {Y – Y} \ \)結線となっている。

ただし，一次側からみた変圧器の\( \ 1 \ \)相当たりの抵抗は\( \ 0.018 \ \mathrm {[\Omega ]} \ \)，リアクタンスは\( \ 8.73 \ \mathrm {[\Omega ]} \ \)，故障が発生した線路の\( \ 1 \ \)線当たりのインピーダンスは\( \ \left( 0.20+\mathrm {j}0.48\right) \ \mathrm {[\Omega / km ]} \ \)とし，変圧器一次電圧側の線路インピーダンス及びその他の値は無視するものとする。次の(a)及び(b)の問に答えよ。

(a)　短絡電流\( \ \mathrm {[kA]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.83 \ \)　　(2)　\( \ 1.30 \ \)　　(3)　\( \ 1.42 \ \)　　(4)　\( \ 4.00 \ \)　　(5)　\( \ 10.5 \ \)

(b)　短絡前に，\( \ 22 \ \mathrm {[kV]} \ \)に保たれていた三相変圧器の母線の線間電圧は，三相短絡故障したとき，何\( \ \mathrm {[kV]} \ \)に低下するか。電圧\( \ \mathrm {[kV]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.72 \ \)　　(2)　\( \ 4.71 \ \)　　(3)　\( \ 10.1 \ \)　　(4)　\( \ 14.2 \ \)　　(5)　\( \ 17.3 \ \)

【ワンポイント解説】

三相短絡事故の事故電流に関する問題です。
本問の場合は，単線図が与えられていないので，自分の手で単線図を描けるかどうかが肝になるかと思います。
また，事故電流は百分率インピーダンスで解くと考える方もいらっしゃるかもしれませんが，本問の場合は百分率インピーダンスを使用しなくても解ける問題となっています。

1.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，それぞれの関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。インピーダンスは電圧を電流で割ったものであるため，一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \)，二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ] &=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ] &=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ] &=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(a)解答：(5)
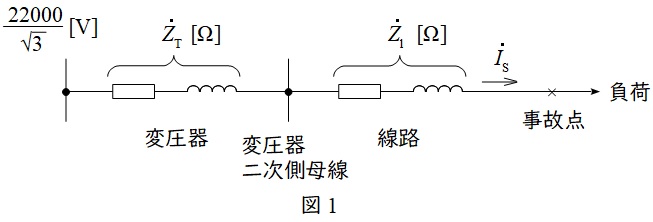
題意に沿って図を描くと図1のようになる。
変圧器の二次側換算のインピーダンス\( \ {\dot Z}_{\mathrm {T}} \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.変圧器の巻数比と変圧比，変流比の関係」の通り，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {T}} &=&\left( \frac {N_{2}}{N_{1}} \right) ^{2} \times \left( 0.018+\mathrm {j}8.73\right) \\[ 5pt ] &=&\left( \frac {V_{2}}{V_{1}} \right) ^{2} \times \left( 0.018+\mathrm {j}8.73\right) \\[ 5pt ] &=&\left( \frac {22\times 10^{3}}{66\times 10^{3}} \right) ^{2} \times \left( 0.018+\mathrm {j}8.73\right) \\[ 5pt ] &=&\frac {1}{9} \times \left( 0.018+\mathrm {j}8.73\right) \\[ 5pt ] &=&0.002+\mathrm {j}0.97 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，変電所から故障点までのインピーダンス\( \ {\dot Z}_{\mathrm {l}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {l}} &=& \left( 0.20+\mathrm {j}0.48\right) \times \frac {500}{1000} \\[ 5pt ] &=&0.10+\mathrm {j}0.24 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，図1より，短絡電流の大きさ\( \ I_{\mathrm {S}} \ \mathrm {[kA]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {S}} &=& \left| \frac {\displaystyle \frac {V_{\mathrm {2n}}}{\sqrt {3}}}{{\dot Z}_{\mathrm {T}}+{\dot Z}_{\mathrm {l}}}\right| \\[ 5pt ] &=& \left| \frac {\displaystyle \frac {22000}{\sqrt {3}}}{0.002+\mathrm {j}0.97+0.10+\mathrm {j}0.24}\right| \\[ 5pt ] &=& \left| \frac {22000}{\sqrt {3}\left( 0.102+\mathrm {j}1.21\right) }\right| \\[ 5pt ] &=& \frac {22000}{\sqrt {3}\sqrt {0.102^{2}+1.21^{2}}} \\[ 5pt ] &≒& \frac {22000}{2.103} \\[ 5pt ] &≒& 10460 \ \mathrm {[A]}　→　10.5 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
(a)の解答及び図1より，変圧器二次側母線電圧の相電圧の大きさ\( \ E_{\mathrm {B}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {B}} &=& \left| {\dot Z}_{\mathrm {l}} \right| I_{\mathrm {S}} \\[ 5pt ] &=& \left| 0.10+\mathrm {j}0.24 \right| \times 10460 \\[ 5pt ] &=& \sqrt {0.10^{2}+0.24^{2}} \times 10460 \\[ 5pt ] &=& 0.26\times 10460 \\[ 5pt ] &≒& 2720 \ \mathrm {[V]}　→　2.720 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，変圧器二次側母線電圧の線間電圧の大きさ\( \ V_{\mathrm {B}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=& \sqrt {3}E_{\mathrm {B}} \\[ 5pt ] &=& \sqrt {3}\times 2720 \\[ 5pt ] &≒& 4711 \ \mathrm {[V]}　→　4.71 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。