Contents
【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ 500 \ \mathrm {kV\cdot A} \ \)の三相変圧器がある。負荷力率が\( \ 1.0 \ \)のときの全負荷銅損が\( \ 6 \ \mathrm {kW} \ \)であった。このときの電圧変動率の値\( \ \mathrm {[%]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,鉄損及び励磁電流は小さく無視できるものとし,簡単のために用いられる電圧変動率の近似式を利用して解答すること。
(1) \( \ 0.7 \ \) (2) \( \ 1.0 \ \) (3) \( \ 1.2 \ \) (4) \( \ 2.5 \ \) (5) \( \ 3.6 \ \)
【ワンポイント解説】
変圧器の電圧変動率に関する問題です。
三相変圧器の出題はあまりないので受験生を迷わせますが,基本的には電圧を相電圧として考えれば単相変圧器と同様に考えて問題ありません。
1.電圧変動率の近似式
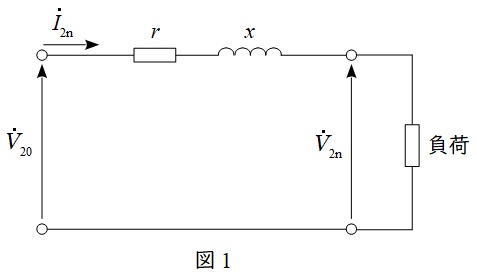
図1のように,変圧器を二次側に換算した回路(\( \ r \ \)は一次二次を合算した抵抗値,\( \ x \ \)は一次二次を合算したリアクタンス値)において,無負荷時の二次端子電圧を\( \ V_{20} \ \),定格負荷時の二次端子電圧を\( \ V_{\mathrm {2n}} \ \)とすると,電圧変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
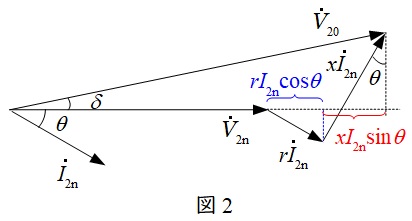
で定義されます。定格二次電流を\( \ I_{\mathrm {2n}} \ \)とするとベクトル図は図2の通りとなります。\( \ V_{20} \ \)と\( \ V_{\mathrm {2n}} \ \)の位相差\( \ \delta \ \)が十分に小さいとすると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≒&\frac {rI_{\mathrm {2n}}\cos \theta +xI_{\mathrm {2n}}\sin \theta }{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&=&\frac {rI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta \times 100 +\frac {xI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \times 100 \\[ 5pt ]
&=&p\cos \theta +q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。上式に出てくる\( \ \displaystyle p=\frac {rI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \ \)は百分率抵抗降下,\( \ \displaystyle q=\frac {xI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \ \)は百分率リアクタンス降下と呼ばれます。
【解答】
解答:(3)
ワンポイント解説「1.電圧変動率の近似式」の通り,電圧変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta +q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,力率\( \ \cos \theta =1 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\varepsilon &≃&p \\[ 5pt ]
\end{eqnarray}
\]
となる。百分率抵抗降下\( \ p \ \)は,三相変圧器であることに注意すると,
\[
\begin{eqnarray}
p &=&\frac {rI_{\mathrm {2n}}}{\displaystyle \frac {V_{\mathrm {2n}}}{\sqrt {3}}} \times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}rI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}rI_{\mathrm {2n}}^{2}}{V_{\mathrm {2n}}I_{\mathrm {2n}}} \times 100 \\[ 5pt ]
&=&\frac {3rI_{\mathrm {2n}}^{2}}{\sqrt {3}V_{\mathrm {2n}}I_{\mathrm {2n}}} \times 100 \\[ 5pt ]
\end{eqnarray}
\]
となり,定格容量\( \ P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {2n}}I_{\mathrm {2n}}=500 \ \mathrm {[kV\cdot A]} \ \),全負荷銅損\( \ P_{\mathrm {c}}=3rI_{\mathrm {2n}}^{2}=6 \ \mathrm {[kW]} \ \)であるから,
\[
\begin{eqnarray}
\varepsilon =p &=&\frac {3rI_{\mathrm {2n}}^{2}}{\sqrt {3}V_{\mathrm {2n}}I_{\mathrm {2n}}} \times 100 \\[ 5pt ]
&=&\frac {6\times 10^{3}}{500\times 10^{3}} \times 100 \\[ 5pt ]
&=&1.2 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは