《電力》〈新エネルギー発電〉[H22:問5]風力発電における風速と出力の関係に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，風力発電に関する記述である。

風として運動している同一質量の空気が持っている運動エネルギーは，風速の\( \ \fbox {　（ア）　} \ \)乗に比例する。また，風として風力発電機の風車面を通過する単位時間当たりの空気の量は，風速の\( \ \fbox {　（イ）　} \ \)乗に比例する。したがって，風車面を通過する空気の持つ運動エネルギーを電気エネルギーに変換する風力発電機の変換効率が風速によらず一定とすると，風力発電機の出力は風速の\( \ \fbox {　（ウ）　} \ \)乗に比例することとなる。

上記の記述中の空白箇所 (ア)，(イ)及び(ウ)に当てはまる数値として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　2　 & 　2　 & 　4　 \\
\hline
(2) & 　2　 & 　1　 & 　3　 \\
\hline
(3) & 　2　 & 　0　 & 　2　 \\
\hline
(4) & 　1　 & 　2　 & 　3　 \\
\hline
(5) & 　1　 & 　1　 & 　2　 \\
\hline
\end{array}
\]

【ワンポイント解説】

風力発電の出力に関する問題です。
ワンポイント解説の風力発電の出力の公式を丸暗記しているのではなく，運動エネルギーと空気量の考え方をマスターした上で公式を理解するようにしないと本問のような問題は解けませんので，中身をしっかりと理解するようにしましょう。

1.風力発電所の出力
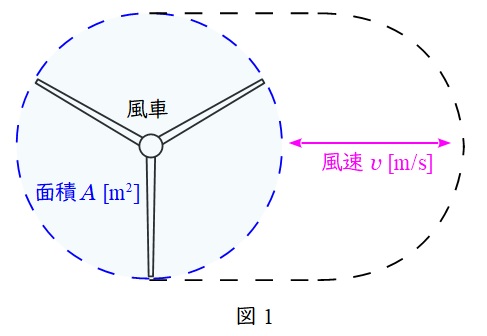
図1に示すように，風車の受風面積を\( \ A \ \mathrm {[m^{2}]} \ \)，風速を\( \ v \ \mathrm {[m／s]} \ \)とすると，単位時間当たりに通過する風の体積\( \ V \ \mathrm {[m^{3}／s]} \ \)は，
\[
\begin{eqnarray}
V &=&Av \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] となります。したがって，単位時間当たりに通過する風の質量\( \ m \ \mathrm {[kg／s]} \ \)は，空気の密度を\( \ \rho \ \mathrm {[kg／m^{3}]} \ \)とすると，
\[
\begin{eqnarray}
m &=&\rho V \\[ 5pt ] &=&\rho Av \ \mathrm {[kg／s]} \\[ 5pt ] \end{eqnarray}
\] となります。物体の運動エネルギーは\( \ \displaystyle E=\frac {1}{2}mv^{2} \ \)であるので，単位時間当たりの風のエネルギー（≒出力）\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\frac {1}{2}mv^{2} \\[ 5pt ] &=&\frac {1}{2}\rho Av^{3} \ \mathrm {[W]}\\[ 5pt ] \end{eqnarray}
\] と求められます。