《機械》〈回転機〉[R4下:問5]三相同期発電機の短絡比の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格出力\( \ 8 \ 000 \ \mathrm {kV\cdot A} \ \)，定格電圧\( \ 6 \ 600 \ \mathrm {V} \ \)の三相同期発電機がある。この発電機の同期インピーダンスが\( \ 4.73 \ \mathrm {\Omega } \ \)のとき，短絡比の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.384 \ \)　　(2)　\( \ 0.665 \ \)　　(3)　\( \ 1.15 \ \)　　(4)　\( \ 1.50 \ \)　　(5)　\( \ 2.61 \ \)

【ワンポイント解説】

三相同期発電機の短絡比を求める問題です。
令和４年上期問5でも類題が出題されていますが，前回は三相短絡電流，今回は同期インピーダンスが分かっているという違いがあります。
別解として百分率インピーダンスを使用した方法も紹介しますので，参考にしてみてください。

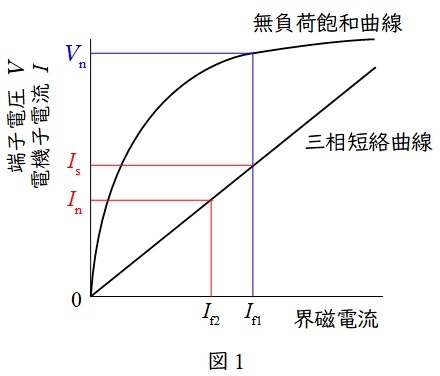
1.同期発電機の無負荷飽和曲線と三相短絡曲線
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
題意より，定格出力\( \ P_{\mathrm {n}}=8 \ 000 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，三相同期発電機の定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {n}} &=& \sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \\[ 5pt ] I_{\mathrm {n}} &=& \frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {8 \ 000\times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ] &≒&699.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，同期インピーダンス\( \ Z_{\mathrm {s}}=4.73 \ \mathrm {[\Omega ]} \ \)より，三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {s}} &=& \frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}}} \\[ 5pt ] &=& \frac {\displaystyle \frac {6 \ 600}{\sqrt {3}}}{4.73} \\[ 5pt ] &≒&805.6 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって短絡比\( \ K \ \)は，ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {805.6}{699.8} \\[ 5pt ] &≒&1.15 \\[ 5pt ] \end{eqnarray}
\] と求められる。

［別解］
発電機の同期インピーダンス\( \ Z_{\mathrm {s}}=4.73 \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス\( \ ％Z_{\mathrm {s}} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {s}} &=& \frac {P_{\mathrm {n}}Z_{\mathrm {s}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=& \frac {8 \ 000\times 10^{3}\times 4.73}{6 \ 600^{2}}\times 100 \\[ 5pt ] &≒&86.87 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であるから，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {100}{％Z_{\mathrm {s}}} \\[ 5pt ] &=& \frac {100}{86.87} \\[ 5pt ] &≒&1.15 \\[ 5pt ] \end{eqnarray}
\] と求められる。