Contents
【問題】
【難易度】★★★★☆(やや難しい)
誘導電動機に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし,誘導電動機の滑りを\( \ s \ \)とする。
(1) 誘導電動機の一次回路には同期速度の回転磁界,二次回路には同期速度の\( \ s \ \)倍の回転磁界が加わる。したがって,一次回路と二次回路の巻数比を\( \ 1 \ \)とした場合,二次誘導起電力の周波数及び電圧は一次誘導起電力の\( \ s \ \)倍となる。
(2) \( \ s \ \)が小さくなると,二次誘導起電力の周波数及び電圧が小さくなるので,二次回路に流れる電流が小さくなる。この変化を電気回路に表現するため,誘導電動機の等価回路では,二次回路の抵抗の値を\( \ \displaystyle \frac {1}{s} \ \)倍にして表現する。
(3) 誘導電動機の等価回路では,一次巻線の漏れリアクタンス,一次巻線の抵抗,二次巻線の漏れリアクタンス,二次巻線の抵抗,及び電動機出力を示す抵抗が直列回路で表されるので,電動機の力率は\( \ 1 \ \)にはならない。
(4) 誘導電動機の等価回路を構成するリアクタンス値及び抵抗値は,電圧が変化しても\( \ s \ \)が一定ならば変わらない。\( \ s \ \)一定で駆動電圧を半分にすれば,等価回路に流れる電流が半分になり,電動機トルクは半分になる。
(5) 同期速度と電動機トルクとで計算される同期ワット(二次入力)は,二次銅損と電動機出力との和となる。
【ワンポイント解説】
内容を理解していてもなかなか正答を導き出すのができないのが本問のような問題です。本問の場合,できるだけ文章を式に直して関係性に気付けるかというところがカギになると思います。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \),回転数が\( \ N \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
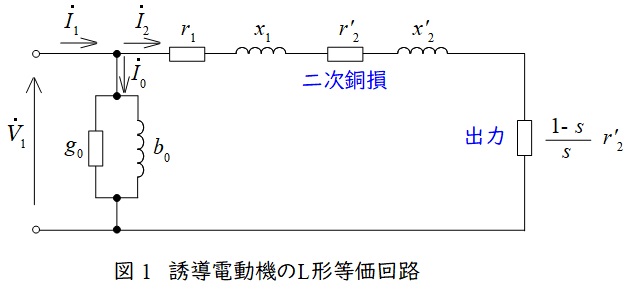
3.誘導電動機のL形等価回路とその特性
誘導電動機のL形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \),二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機に発生するトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=& \frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=& 3\frac {r_{2}^{\prime }}{\omega _{\mathrm {s}}s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
【解答】
解答:(4)
(1)正しい
問題文の通りです。二次回路に加わる回転磁界の回転速度は,同期速度\( \ N_{\mathrm {s}} \ \)と回転数\( \ N \ \)の差になりますが,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
N_{\mathrm {s}}-N &=&sN_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
なので,二次回路には同期速度の\( \ s \ \)倍の回転磁界が加わります。
また,誘導電動機の二次側の誘導起電力及び周波数は一次側の\( \ s \ \)倍となります。
(2)正しい
問題文の通り,\( \ s \ \)が小さくなると,二次誘導起電力の周波数及び電圧が小さくなるので,二次回路に流れる電流が小さくなります。ワンポイント解説「3.誘導電動機のL形等価回路とその特性」では二次側抵抗と出力の抵抗を分けて考えていますが,足し合わせると,
\[
\begin{eqnarray}
{r_{2}}^{\prime } +\frac {1-s}{s}{r_{2}}^{\prime } &=&\frac {{r_{2}}^{\prime }}{s} \\[ 5pt ]
\end{eqnarray}
\]
となり,二次回路の抵抗は\( \ \displaystyle \frac {1}{s} \ \)倍にして表現されることが分かります。
(3)正しい
問題文の通り,誘導電動機の等価回路では,一次巻線の漏れリアクタンス,一次巻線の抵抗,二次巻線の漏れリアクタンス,二次巻線の抵抗,及び電動機出力を示す抵抗が直列回路で表されるので,電動機の力率は\( \ 1 \ \)にはならず,必ず遅れ力率となります。
(4)誤り
問題文の通り,誘導電動機の等価回路を構成するリアクタンス値及び抵抗値は,電圧が変化しても\( \ s \ \)が一定ならば変化しません。また,\( \ s \ \)一定で駆動電圧を半分にすると,等価回路に流れる電流はオームの法則により半分になります。しかしながら,ワンポイント解説「3.誘導電動機のL形等価回路とその特性」の通り,電動機のトルクは二次電流の2乗に比例するので,電圧が半分になるとトルクは4分の1になります。
(5)正しい
問題文の通り,同期速度と電動機トルクとで計算される同期ワット(二次入力)は,ワンポイント解説「3.誘導電動機のL形等価回路とその特性」の通り,
\[
\begin{eqnarray}
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,二次銅損と電動機出力との和となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは