《機械》〈電動機応用〉[H28:問11]エレベータを上昇するための出力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

かごの質量が\( \ \mathrm {200 \ kg} \ \)，定格積載質量が\( \ \mathrm {1000 \ kg} \ \)のロープ式エレベータにおいて，釣合いおもりの質量は，かごの質量に定格積載質量の\( \ \mathrm {40 \ ％} \ \)を加えた値とした。このエレベータで，定格積載質量を搭載したかごを一定速度\( \ \mathrm {90 \ m/min} \ \)で上昇させるときに用いる電動機の出力の値\( \ \mathrm {[ kW ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，機械効率は\( \ 75 \ \)％，加減速に要する動力及びロープの質量は無視するものとする。

(1)　\( \ 1.20 \ \)　　(2)　\( \ 8.82 \ \)　　(3)　\( \ 11.8 \ \)　　(4)　\( \ 23.5 \ \)　　(5)　\( \ 706 \ \)

【ワンポイント解説】

力学の問題まで出題されるという機械科目の出題範囲の広さを感じさせる問題です。問題はそれほど難しくはないですが，なかなか電験の教科書に記載されていない内容です。あと，本問は重力加速度\( \ g=9.8 \ \mathrm {m/s^{2}} \ \)は与えられていませんが，常識的に知っておいて下さい。

1.物体上昇時に必要なエネルギー\( \ E \ \)
質量\( \ M \ \)を高さ\( \ h \ \)持ち上げるのに必要なエネルギー\( \ E \ \)は，
\[
\begin{eqnarray}
E&=&Mgh \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
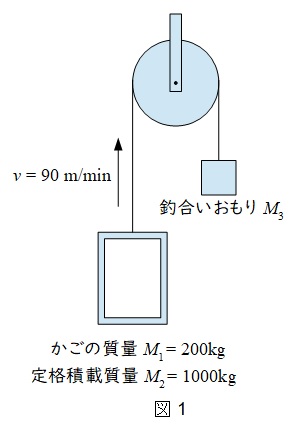
題意に沿って図を描くと図1のようになる。
釣合いおもりの質量\( \ M_{3} \ \)は，題意より，
\[
\begin{eqnarray}
M_{3}&=&M_{1}+0.4M_{2} \\[ 5pt ] &=& 200+0.4\times 1000 \\[ 5pt ] &=&600 \ \mathrm {[ kg ]} \\[ 5pt ] \end{eqnarray}
\] となる。エレベータを動かす速度\( \ v \ \mathrm {[ m/s ]} \ \)は，
\[
\begin{eqnarray}
v&=&\frac {90}{60} \\[ 5pt ] &=&1.5 \ \mathrm {[ m/s ]}
\end{eqnarray}
\] となる。エレベータを持ち上げるのに必要な動力\( \ P_{0} \ \)は単位時間当たりに持ち上げるエネルギーであるから，
\[
\begin{eqnarray}
P_{0}&=&\left( M_{1}+M_{2}-M_{3}\right) g v \\[ 5pt ] &=&\left( 200+1000-600\right) \times 9.8 \times 1.5 \\[ 5pt ] &=&8820\mathrm \ {[ W ]}　→　8.82 \ \mathrm {[ kW ]}
\end{eqnarray}
\] と求められる。機械効率が75％であるから，電動機の出力\( \ P \ \)は，
\[
\begin{eqnarray}
P&=&\frac {P_{0}}{0.75} \\[ 5pt ] &=&\frac {8.82}{0.75} \\[ 5pt ] &=&11.76 →　11.8 \ \mathrm {[ kW ]}
\end{eqnarray}
\] と求められる。