Contents
【問題】
【難易度】★★★★☆(やや難しい)
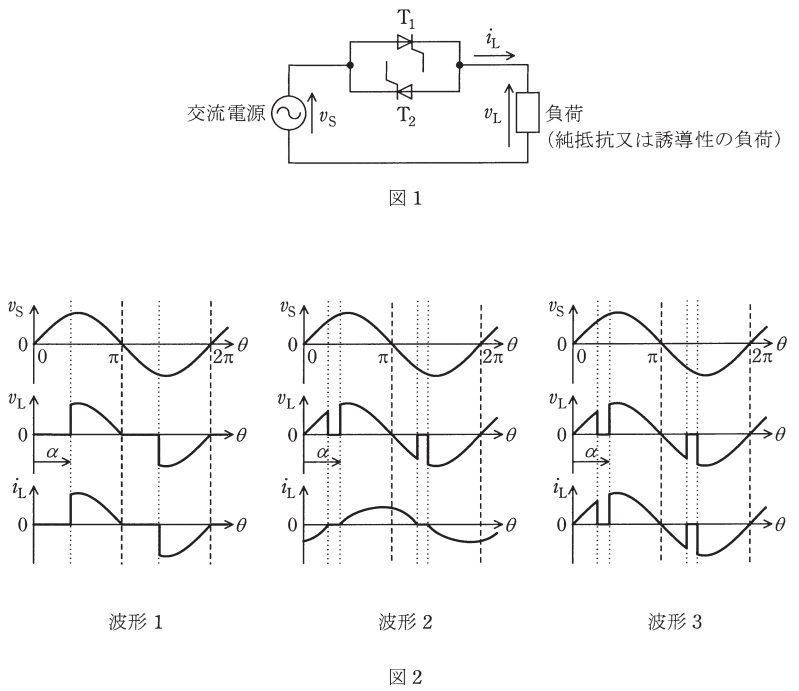
図1に示す単相交流電力調整回路が制御遅れ角\( \ \alpha \ [\mathrm {rad}] \ \)で運転しているときの動作を考える。
正弦波の交流電源電圧は\( \ v_{\mathrm {S}} \ \),負荷は純抵抗負荷又は誘導性負荷であり,負荷電圧を\( \ v_{\mathrm {L}} \ \),負荷電流を\( \ i_{\mathrm {L}} \ \)とする。次の(a)及び(b)の問に答えよ。
(a) 図2の波形1~3のうち,純抵抗負荷の場合と誘導性負荷の場合とで発生する波形の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 純抵抗負荷 & 誘導性負荷 \\
\hline
(1) & 波形1 & 波形2 \\
\hline
(2) & 波形1 & 波形3 \\
\hline
(3) & 波形2 & 波形1 \\
\hline
(4) & 波形2 & 波形3 \\
\hline
(5) & 波形3 & 波形2 \\
\hline
\end{array}
\]
(b) 交流電源電圧\( \ v_{\mathrm {S}} \ \)の実効値を\( \ V_{\mathrm {S}} \ \)として,純抵抗負荷の場合の負荷電圧\( \ v_{\mathrm {L}} \ \)の実効値\( \ V_{\mathrm {L}} \ \)は,\( \ \displaystyle V_{\mathrm {L}}=V_{\mathrm {S}}\sqrt {1-\frac {\alpha }{\pi}+\frac {\sin 2\alpha }{2\pi }} \ \)で表される。制御遅れ角を\( \ \displaystyle \alpha _{1}=\frac {\pi }{2} \ [\mathrm {rad}] \ \)から\( \ \displaystyle \alpha _{2}=\frac {\pi }{4} \ [\mathrm {rad}] \ \)に変えたときに,負荷の抵抗で消費される交流電力は何倍となるか,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.550 \ \) (2) \( \ 0.742 \ \) (3) \( \ 1.35 \ \) (4) \( \ 1.82 \ \) (5) \( \ 2.00 \ \)
【ワンポイント解説】
問題図のような回路を交流電力調整回路と言い,静止形無効電力調整装置(\( \ \mathrm {TSC} \ \),\( \ \mathrm {TCR} \ \))やサイクロコンバータに利用されます。(a)は交流電力調整回路のメカニズムに関する問題です。(b)は一見難しそうに見えますが,中身は数値計算の問題となります。
1.交流電力調整回路の原理
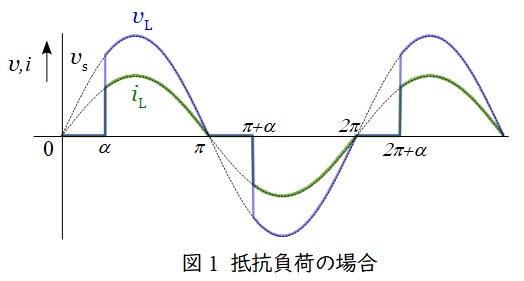
まず,抵抗負荷の場合について説明します。
問題の図の回路に電圧\( \ v_{\mathrm {S}} \ \)をかけると,制御角\( \ \alpha \ \)でサイリスタ\( \ T_{1} \ \)が\( \ \mathrm {ON} \ \)となります。それにより,\( \ v_{\mathrm {L}} \ \)が印加され,抵抗負荷なので,\( \ i_{\mathrm {L}} \ \)も同位相の電流が流れます。その後,\( \ \pi \ \)になると,逆電圧がかかり\( \ i_{\mathrm {L}} \ \)が\( \ 0 \ \)となるため,サイリスタ\( \ T_{1} \ \)が\( \ \mathrm {OFF} \ \)となります。
\( \ \pi +\alpha \ \)になると,\( \ T_{2} \ \)が\( \ \mathrm {ON} \ \)となり,\( \ 2\pi \ \)になると,\( \ T_{2} \ \)が\( \ \mathrm {OFF} \ \)となり,その後,同じ動作を繰り返します。よって,波形は図1のようになります。
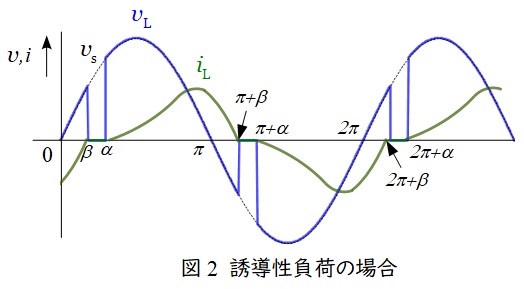
次に,誘導性負荷の場合について説明します。
誘導性負荷の場合,電圧をかけることによって,誘導性負荷にエネルギーが蓄積されることが特徴となります。
まず,抵抗負荷と同様に制御角\( \ \alpha \ \)でサイリスタ\( \ T_{1} \ \)が\( \ \mathrm {ON} \ \)となります。しかし,誘導性負荷の場合,その特性により電流値は急激に上がらず,抵抗負荷よりもゆっくり上がります。その後,\( \ v_{\mathrm {L}} \ \)は抵抗負荷と同様に,電流\( \ i_{\mathrm {L}} \ \)は遅れて徐々に上昇し,\( \ \pi \ \)になると逆電圧がかかりますが,誘導性負荷に蓄積されたエネルギーによって電流は流れるため,電流が\( \ 0 \ \)になる\( \ \pi +\beta \ \)まで\( \ T_{1} \ \)が\( \ \mathrm {ON} \ \)のままとなります。
\( \ \pi +\alpha \ \)になると,抵抗負荷と同様に\( \ T_{2} \ \)が\( \ \mathrm {ON} \ \)となり,その後は同じ動作を繰り返します。よって,波形は図2のようになります。
【解答】
(a)解答:(1)
ワンポイント解説「1.交流電力調整回路の原理」の通り,抵抗負荷の場合が波形\( \ 1 \ \),誘導性負荷の場合が波形\( \ 2 \ \)となります。
(b)解答:(4)
題意より,抵抗負荷での抵抗値を\( \ R \ \)とすると,電流の実効値\( \ I_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&\frac {V_{\mathrm {L}}}{R} \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}}{R}\sqrt {1-\frac {\alpha }{\pi}+\frac {\sin 2\alpha }{2\pi }} \\[ 5pt ]
\end{eqnarray}
\]
となるので,消費電力\( \ P_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&RI_{\mathrm {L}}^{2} \\[ 5pt ]
&=&R\left( \frac {V_{\mathrm {S}}}{R}\sqrt {1-\frac {\alpha }{\pi}+\frac {\sin 2\alpha }{2\pi }}\right) ^{2} \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( 1-\frac {\alpha }{\pi}+\frac {\sin 2\alpha }{2\pi }\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \displaystyle \alpha _{1}=\frac {\pi }{2} \ [\mathrm {rad}] \ \)と\( \ \displaystyle \alpha _{2}=\frac {\pi }{4} \ [\mathrm {rad}] \ \)の時の消費電力\( \ P_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}}(\alpha _{1})&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( 1-\frac {\displaystyle \frac {\pi }{2} }{\pi}+\frac {\displaystyle \sin 2\cdot \frac {\pi }{2}}{2\pi }\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( 1-\frac {1}{2}+0\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}^{2}}{2R} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
P_{\mathrm {L}}(\alpha _{2})&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( 1-\frac {\displaystyle \frac {\pi }{4} }{\pi}+\frac {\displaystyle \sin 2\cdot \frac {\pi }{4}}{2\pi }\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( 1-\frac {1}{4}+\frac {1}{2\pi }\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {S}}^{2}}{R}\left( \frac {3}{4}+\frac {1}{2\pi }\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ P_{\mathrm {L}}(\alpha _{1}) \ \)と\( \ P_{\mathrm {L}}(\alpha _{2}) \ \)の比は,
\[
\begin{eqnarray}
\frac {P_{\mathrm {L}}(\alpha _{2})}{P_{\mathrm {L}}(\alpha _{1})}&=&\frac {\displaystyle \frac {V_{\mathrm {S}}^{2}}{R}\left( \frac {3}{4}+\frac {1}{2\pi }\right) }{\displaystyle \frac {V_{\mathrm {S}}^{2}}{2R}} \\[ 5pt ]
&=&2\times \left( \frac {3}{4}+\frac {1}{2\pi }\right) \\[ 5pt ]
&=&\frac {3}{2}+\frac {1}{\pi } \\[ 5pt ]
&≒&1.82 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。




















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは