Contents
【問題】
【難易度】★★★★☆(やや難しい)
電気計測に関する記述について,次の(a)及び(b)に答えよ。
(a) ある量の測定に用いる方法には各種あるが,指示計器のように測定量を指針の振れの大きさに変えて,その指示から測定量を知る方法を\( \ \fbox { (ア) } \ \)法という。これに比較して精密な測定を行う場合に用いられている\( \ \fbox { (イ) } \ \)法は,測定量と同種類で大きさを調整できる既知量を別に用意し,既知量を測定量に平衡させて,そのときの既知量の大きさから測定量を知る方法である。\( \ \fbox { (イ) } \ \)法を用いた測定器の例としては,ブリッジや\( \ \fbox { (ウ) } \ \)がある。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & 偏 位 & 零 位 & 直流電位差計 \\
\hline
(2) & 偏 位 & 差 動 & 誘導形電力量計 \\
\hline
(3) & 間 接 & 零 位 & 直流電位差計 \\
\hline
(4) & 間 接 & 差 動 & 誘導形電力量計 \\
\hline
(5) & 偏 位 & 零 位 & 誘導形電力量計 \\
\hline
\end{array}
\]
(b) 図は,ケルビンダブルブリッジの原理図である。図において\( \ R_{x} \ \mathrm {[\Omega ]} \ \)が未知の抵抗,\( \ R_{s} \ \mathrm {[\Omega ]} \ \)は可変抵抗,\( \ P \ \mathrm {[\Omega ]} \ \), \( \ Q \ \mathrm {[\Omega ]} \ \),\( \ p \ \mathrm {[\Omega ]} \ \),\( \ q \ \mathrm {[\Omega ]} \ \)は固定抵抗である。このブリッジは,抵抗\( \ R_{x} \ \mathrm {[\Omega ]} \ \)のリード線の抵抗が,固定抵抗\( \ r \ \mathrm {[\Omega ]} \ \)及び直流電源側の接続線に含まれる回路構成となっており,低い抵抗の測定に適している。
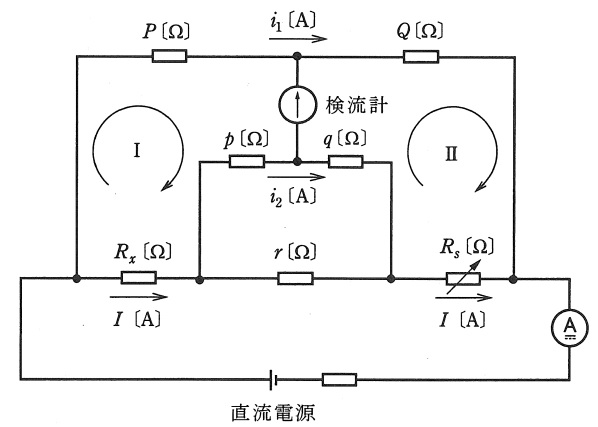
図の回路において,固定抵抗\( \ P \ \mathrm {[\Omega ]} \ \), \( \ Q \ \mathrm {[\Omega ]} \ \),\( \ p \ \mathrm {[\Omega ]} \ \),\( \ q \ \mathrm {[\Omega ]} \ \)の抵抗値が\( \ \fbox { (ア) } \ =0 \ \)の条件を満たしていて,可変抵抗\( \ R_{s} \ \mathrm {[\Omega ]} \ \),固定抵抗\( \ r \ \mathrm {[\Omega ]} \ \)においてブリッジが平衡している。この場合は,次式から抵抗\( \ R_{x} \ \mathrm {[\Omega ]} \ \)が求まる。
\[
\begin{eqnarray}
R_{x} &=&\left( \ \fbox { (イ) } \ \right) R_{s} \\[ 5pt ]
\end{eqnarray}
\]
この式が求まることを次の手順で証明してみよう。
〔証明〕
回路に流れる電流を図に示すように\( \ I \ \mathrm {[A]} \ \),\( \ i_{1} \ \mathrm {[A]} \ \),\( \ i_{2} \ \mathrm {[A]} \ \)とし,閉回路Ⅰ及びⅡにキルヒホッフの第\( \ 2 \ \)法則を適用すると式 ①,②が得られる。
\[
\begin{eqnarray}
Pi_{1} &=&R_{x}I+pi_{2} &・・・・・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
Qi_{1} &=&R_{s}I+qi_{2} &・・・・・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
式①,②から
\[
\begin{eqnarray}
\frac {P}{Q} &=&\frac {R_{x}I+pi_{2}}{R_{s}I+qi_{2}}=\frac {\displaystyle R_{x}+p\frac {i_{2}}{I}}{\displaystyle R_{s}+q\frac {i_{2}}{I}} ・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
また,\( \ I \ \)は\( \ \left( p+q\right) \ \)と\( \ r \ \)の回路に分流するので,\( \ \left( p+q\right) i_{2}=r\left( I-i_{2}\right) \ \)の関係から式④が得られる。
\[
\begin{eqnarray}
\frac {i_{2}}{I} &=& \ \fbox { (ウ) } \ ・・・・・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
ここで,\( \ K= \ \fbox { (ウ) } \ \)とし,式③を整理すると式⑤が得られ,抵抗\( \ R_{x} \ \mathrm {[\Omega ]} \ \)が求まる。
\[
\begin{eqnarray}
R_{x} &=&\left( \ \fbox { (イ) } \ \right) R_{s}+\left( \ \fbox { (ア) } \ \right) qK ・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる式として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & \displaystyle \frac {P}{Q}-\frac {p}{q} & \displaystyle \frac {P}{Q} & \displaystyle \frac {r}{p+q+r} \\
\hline
(2) & \displaystyle \frac {p}{q}-\frac {P}{Q} & \displaystyle \frac {P}{q} & \displaystyle \frac {p}{p+r} \\
\hline
(3) & \displaystyle \frac {p}{q}-\frac {P}{Q} & \displaystyle \frac {Q}{p} & \displaystyle \frac {q}{q+r} \\
\hline
(4) & \displaystyle \frac {Q}{P}-\frac {q}{p} & \displaystyle \frac {Q}{P} & \displaystyle \frac {r}{p+q+r} \\
\hline
(5) & \displaystyle \frac {P}{Q}-\frac {p}{q} & \displaystyle \frac {P}{Q} & \displaystyle \frac {p}{p+q+r} \\
\hline
\end{array}
\]
【ワンポイント解説】
偏位法と零位法の特徴及び,ケルビンダブルブリッジの抵抗値の導出方法に関する問題です。
じっくりと取り組めばそれほど難解ではありませんが,問題文が長いため短い時間で解こうとすると読解と式変形に時間を要する問題と言えるかと思います。
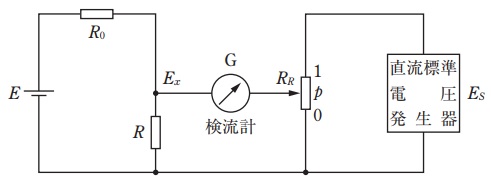
1.直流電位差計(零位法の例)
直流電位差計は下図のように,直流電圧発生器とすべり抵抗器を用いて電圧を測定するものです。
直流電圧\( \ E_{s} \ \)を発生して,すべり抵抗器の位置\( \ p \left( 0≦p≦1 \right) \ \)にしたとき検流計に電流が流れなかったとき,測定電圧\( \ E_{x} \ \)は,
\[
\begin{eqnarray}
E_{x} &=& pE_{s} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
出典:電気工学ハンドブック(第7版) 一般社団法人電気学会 オーム社 P.270
2.電流力計形計器(偏位法の例)
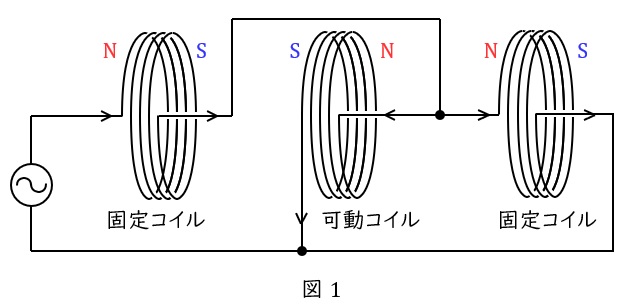
図1のように三つのコイルを配置し,中央のコイルを可動式にし,両端のコイルを固定式にします。
それぞれのコイルには右ねじの法則により磁界が発生し磁化されますが,可動コイルだけ電流を逆向きに流すことにより,それぞれに反発力が生まれます。
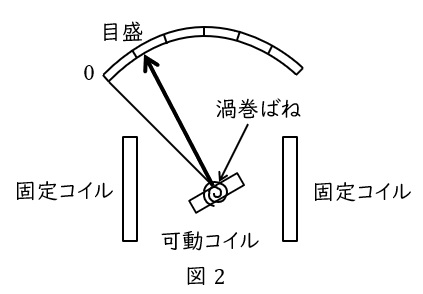
反発力の大きさが測定する電流の大きさに比例するので,図2のように可動コイルに指針をつけ軸で回転させることにより,電流の大きさや負荷電力の大きさを測定することが可能となります。また,電流がなくなった場合に元の位置に戻るように渦巻ばねが設けられています。
逆向きに流れてもすべての\( \ \mathrm {N} \ \)極と\( \ \mathrm {S} \ \)極が反転し同様の反発力が発生するため,直流・交流ともに測定可能となります。
3.直流ブリッジの平衡条件
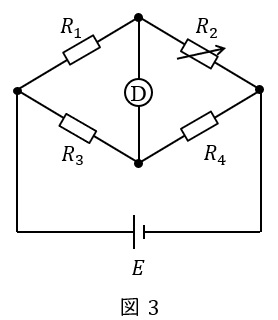
直流ブリッジ回路は抵抗の抵抗値を求める方法であり,ホイートストンブリッジと呼ばれます。
図3の回路において,検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い,
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。したがって,3つの既知の抵抗があれば,残りの1つの抵抗値を求めることができます。
【解答】
(a)解答:(1)
(ア)
ワンポイント解説「2.電流力計形計器(偏位法の例)」の通り,指示計器のように測定量を指針の振れの大きさに変えて,その指示から測定量を知る方法を偏位法といいます。
(イ)
ワンポイント解説「1.直流電位差計(零位法の例)」の通り,測定量と同種類で大きさを調整できる既知量を別に用意し,既知量を測定量に平衡させて,そのときの既知量の大きさから測定量を知る方法を零位法といいます。
(ウ)
ワンポイント解説「1.直流電位差計(零位法の例)」の通り,零位法を用いた測定器としては直流電位差計があります。
(b)解答:(1)
題意より,\( \ \left( p+q\right) i_{2}=r\left( I-i_{2}\right) \ \)の関係があるから,これを整理すると,
\[
\begin{eqnarray}
\left( p+q\right) i_{2} &=&r\left( I-i_{2}\right) \\[ 5pt ]
pi_{2}+qi_{2} &=&rI-ri_{2} \\[ 5pt ]
pi_{2}+qi_{2}+ri_{2} &=&rI \\[ 5pt ]
\left( p+q+r\right) i_{2} &=&rI \\[ 5pt ]
\frac {i_{2}}{I} &=&\frac {r}{p+q+r} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle K=\frac {i_{2}}{I}=\frac {r}{p+q+r} \ \)とし,式③を整理すると,
\[
\begin{eqnarray}
\frac {P}{Q} &=&\frac {\displaystyle R_{x}+p\frac {i_{2}}{I}}{\displaystyle R_{s}+q\frac {i_{2}}{I}} \\[ 5pt ]
&=&\frac {\displaystyle R_{x}+pK}{\displaystyle R_{s}+qK} \\[ 5pt ]
\frac {P}{Q}\left( R_{s}+qK\right) &=&R_{x}+pK \\[ 5pt ]
R_{x}&=&\frac {P}{Q}\left( R_{s}+qK\right) -pK \\[ 5pt ]
&=&\frac {P}{Q}R_{s}+\frac {P}{Q}qK-pK \\[ 5pt ]
&=&\frac {P}{Q}R_{s}+\left( \frac {P}{Q}-\frac {p}{q}\right) qK \\[ 5pt ]
\end{eqnarray}
\]
とな。よって,(ア)が\( \ \displaystyle \frac {P}{Q}-\frac {p}{q} \ \),(イ)が\( \ \displaystyle \frac {P}{Q} \ \),(ウ)が\( \ \displaystyle \frac {r}{p+q+r} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは