《理論》〈電気回路〉[H27:問7]直流回路のインピーダンスに関する論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

以下の記述で，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　直流電圧源と抵抗器，コンデンサが直列に接続された回路のコンデンサには，定常状態では電流が流れない。

(2)　直流電圧源と抵抗器，コイルが直列に接続された回路のコイルの両端の電位差は，定常状態では零である。

(3)　電線の抵抗値は，長さに比例し，断面積に反比例する。

(4)　並列に接続した二つの抵抗器\(R_{1}\)，\(R_{2}\)を一つの抵抗器に置き換えて考えると，合成抵抗の値は\(R_{1}\)，\(R_{2}\)の抵抗値の逆数の和である。

(5)　並列に接続した二つのコンデンサ\(C_{1}\)，\(C_{2}\)を一つのコンデンサに置き換えて考えると，合成静電容量は\(C_{1}\)，\(C_{2}\)の静電容量の和である。

【ワンポイント解説】

誤答選択問題は慎重に読み進めないと間違いに気が付きません。本問もサラッと読むと正しいかなっと思ってしまう典型的な問題と言えると思います。

1.並列回路の合成抵抗と合成静電容量
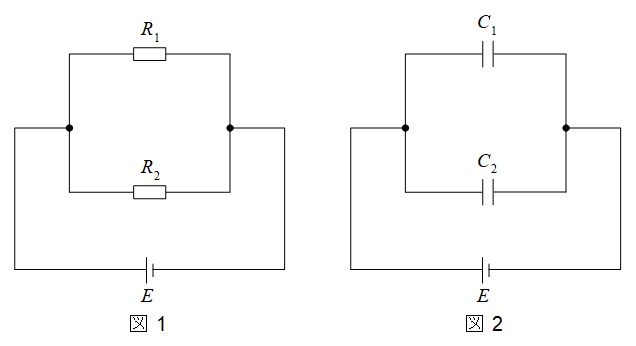
図1の回路において，\(R_{1}\)と\(R_{2}\)の合成抵抗は，
\[
\begin{eqnarray}
\left( \frac {1}{R_{1}}+\frac {1}{R_{2}}\right) ^{-1}&=&\left( \frac {R_{1}+R_{2}}{R_{1}R_{2}}\right) ^{-1} \\[ 5pt ] &=&\frac {R_{1}R_{2}}{R_{1}+R_{2}}
\end{eqnarray}
\] となります。
また，図2の回路において，\(C_{1}\)と\(C_{2}\)の合成静電容量は，
\[
C_{1}+C_{2}
\] となります。

【解答】

解答：(4)
(1)：正しい
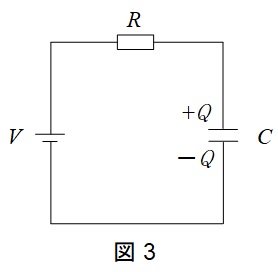
図3の回路において，定常状態では，\(Q=CV\)の電荷が蓄えられ，コンデンサ間の電位差と電源の電圧が等しくなるので，電流は流れなくなります。

(2)：正しい
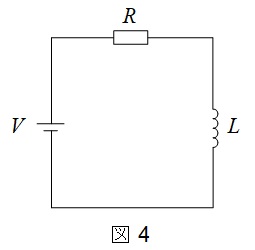
図4の回路において，コイルに現れる電圧は電流変化に比例する。定常状態では電流変化はないので，コイルの両端に電位差は零となる。

(3)：正しい
電線の抵抗値\(R \ [\Omega ]\)は，電線の抵抗率\(\rho \ [\Omega \cdot \mathrm {m} ]\)，断面積\(S \ [ \mathrm {m^{2}} ]\)，長さ\(l \ \mathrm {[m]}\)とすると，
\[
R=\rho \frac {l}{S}
\] となるので，長さに比例し，断面積に反比例する。

　※　水を流すホースをイメージすると分かりやすいです。ホースが長く，断面積が小さい方が水を流しにくいと思います。

(4)：誤り
ワンポイント解説「1.並列回路の合成抵抗と合成静電容量」の通り，合成抵抗は，\(R_{1}\)，\(R_{2}\)の抵抗値の逆数の和の逆数となる。

(5)：正しい
ワンポイント解説「1.並列回路の合成抵抗と合成静電容量」の通り，合成抵抗の値は\(C_{1}\)，\(C_{2}\)の静電容量の和となる。