《理論》〈電磁気〉[H20:問3]環状ソレノイドの起磁力と鉄心中の磁束に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

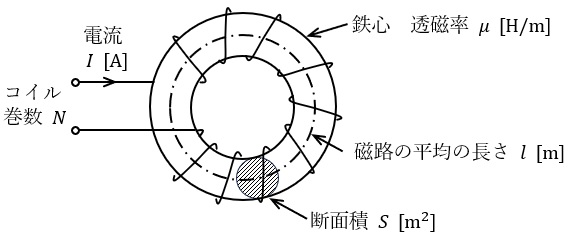
図のように，磁路の平均の長さ\( \ l \ \mathrm {[m]} \ \)，断面積\( \ S \ \mathrm {[m^{2}]} \ \)で透磁率\( \ \mu \ \mathrm {[H / m]} \ \)の環状鉄心に巻数\( \ N \ \)のコイルが巻かれている。この場合，環状鉄心の磁気抵抗は\( \ \displaystyle \frac {l}{\mu S} \ \mathrm {[A / Wb]} \ \)である。いま，コイルに流れている電流を\( \ I \ \mathrm {[A]} \ \)としたとき，起磁力は\( \ \fbox {　 （ア） 　} \ \mathrm {[A]} \ \)であり，したがって，磁束は\( \ \fbox {　 （イ） 　} \ \mathrm {[Wb]} \ \)となる。

ただし，鉄心及びコイルの漏れ磁束はないものとする。

上記の記述中の空白箇所(ア)及び(イ)に当てはまる式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{ccc}
& （ア） & （イ） \\
\hline
(1) & 　I　 & 　\displaystyle \frac {l}{\mu S}I　 \\
\hline
(2) & 　I　 & 　\displaystyle \frac {\mu S}{l}I　 \\
\hline
(3) & 　NI　 & 　\displaystyle \frac {lN}{\mu S}I　 \\
\hline
(4) & 　NI　 & 　\displaystyle \frac {\mu SN}{l}I　 \\
\hline
(5) & 　N^{2}I　 & 　\displaystyle \frac {\mu SN^{2}}{l}I　 \\
\hline
\end{array}
\]

【ワンポイント解説】

環状ソレノイドの起磁力と鉄心中の磁束を求める問題です。
磁気回路のオームの法則を知っていれば解ける，電験としてはかなり易しい問題となります。
こういう問題をミスで取りこぼさないようにすることが，電験合格の近道となります。

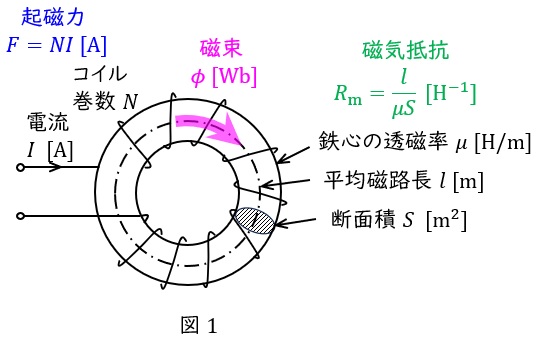
1.磁気回路のオームの法則
中心長さ\( \ l \ \mathrm {[ m ]} \ \)の環状鉄心に巻き数\( \ N \ \)のコイルが巻かれ，そこに電流\( \ I \ \mathrm {[ A ]} \ \)が流れている時，鉄心内の磁界の強さ\( \ H \ \mathrm {[ A / m ]} \ \)は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄心内の磁束密度\( \ B \ \mathrm {[ T ]} \ \)は，鉄心内の透磁率\( \ \mu \ \mathrm {[ H / m ]} \ \)とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。鉄心内の磁束\( \ \phi \ \mathrm {[ Wb ]} \ \)は，鉄心の断面積\( \ S \ \mathrm {[ m^{2} ]} \ \)とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] \end{eqnarray}
\] となり，起磁力\( \ F=NI \ \mathrm {[ A ]} \ \)，磁気抵抗\( \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \mathrm {[ H^{-1} ]} \ \)とすると，
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，磁気回路のオームの法則が成立します。

【解答】

解答：(4)
(ア)
ワンポイント解説「1.磁気回路のオームの法則」の通り，起磁力は\( \ NI \ \mathrm {[A]} \ \)となります。

(イ)
ワンポイント解説「1.磁気回路のオームの法則」の通り，磁束\( \ \phi \ \mathrm {[Wb]} \ \)は，
\[
\begin{eqnarray}
\phi &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] &=&\displaystyle \frac {\mu SN}{l}I \\[ 5pt ] \end{eqnarray}
\] となります。