《理論》〈電気及び電子計測〉[H28:問16]測定誤差に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

図のような回路において，抵抗\( \ \mathrm {R} \ \)の値\( \ \mathrm { [ \Omega ] } \ \)を電圧降下法によって測定した。この測定で得られた値は，電流計\( \ I=1.600 \ \mathrm {A} \ \)，電圧計\( \ V=50.00 \ \mathrm {V} \ \)であった。次の(a)及び(b)の問に答えよ。
ただし，抵抗\( \ \mathrm {R} \ \)の真の値は\( \ \mathrm {31.21 \ \Omega } \ \)とし，直流電源，電圧計及び電流計の内部抵抗の影響は無視できるものである。また，抵抗\( \ \mathrm {R} \ \)の測定値は有効数字4桁で計算せよ。

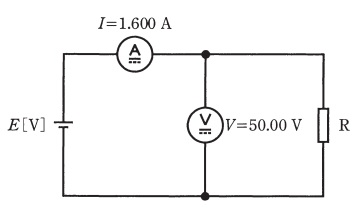
(a)　抵抗\( \ \mathrm {R} \ \)の絶対誤差\( \ \mathrm { [ \Omega ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.004 \ \)　　(2)　\( \ 0.04 \ \)　　(3)　\( \ 0.14 \ \)　　(4)　\( \ 0.4 \ \)　　(5)　\( \ 1.4 \ \)

(b)　絶対誤差の真の値に対する比率を相対誤差という。これを百分率で示した，抵抗\( \ \mathrm {R} \ \)の百分率誤差(誤差率)\( \ \mathrm {[ ％ ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.0013 \ \)　　(2)　\( \ 0.03 \ \)　　(3)　\( \ 0.13 \ \)　　(4)　\( \ 0.3 \ \)　　(5)　\( \ 1.3 \ \)

【ワンポイント解説】

本問は平成28年度の問題で最も正答率が高い問題であると思います。こういう問題の取りこぼしを防ぐことが電験三種合格への道となります。

1.誤差及び誤差率の定義
真値を\( \ T \ \)，測定値を\( \ M \ \)とすると，誤差\( \ \varepsilon \ \)と誤差率\( \ ％\varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ] ％\varepsilon &=&\frac {M-T}{T} \times 100 [％] \end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
抵抗\( \ \mathrm {R} \ \)の測定値\( \ M \ \)は，
\[
\begin{eqnarray}
M&=&\frac {50.00}{1.600} \\[ 5pt ] &=&31.25 \ [ \Omega ] \\[ 5pt ] \end{eqnarray}
\] であるから，誤差\(\varepsilon \)は，
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ] &=&31.25-31.21 \\[ 5pt ] &=&0.04 \ [ \Omega ] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
抵抗\( \ R \ \)の百分率誤差\( \ ％\varepsilon \ \)は，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {M-T}{T} \times 100 \\[ 5pt ] &=&\frac {0.04}{31.21} \times 100 \\[ 5pt ] &≒&0.128　→　0.13 [％] \end{eqnarray}
\] と求められる。