Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図のように,\( \ 2 \ \)種類の直流電源と\( \ 3 \ \)種類の抵抗からなる回路がある。各抵抗に流れる電流を図に示す向きに定義するとき,電流\( \ I_{1} \ \mathrm {[A]} \ \),\( \ I_{2} \ \mathrm {[A]} \ \),\( \ I_{3} \ \mathrm {[A]} \ \)の値として,正しいものを組み合わせたのは次のうちどれか。
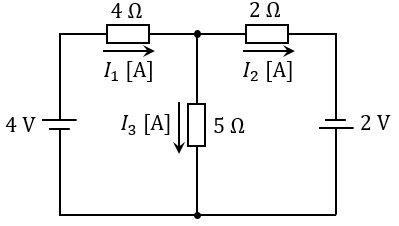
\[
\begin{array}{cccc}
& I_{1} & I_{2} & I_{3} \\
\hline
(1) & -1 & -1 & 0 \\
\hline
(2) & -1 & 1 & -2 \\
\hline
(3) & 1 & 1 & 0 \\
\hline
(4) & 2 & 1 & 1 \\
\hline
(5) & 1 & -1 & 2 \\
\hline
\end{array}
\]
【ワンポイント解説】
\( \ 2 \ \)個の直流電源と\( \ 3 \ \)つの抵抗を直並列させた回路の各抵抗に流れる電流値を導出する問題です。
重ね合わせの理を用いて解いても良いと思いますが,\( \ I_{1} \ \)と\( \ I_{2} \ \)の流れる各電源と抵抗の大きさの比が等しいことに気付き,ミルマンの定理を適用して\( \ I_{3} \ \)を求めるとさらに早く解ける問題となるかと思います。
1.重ね合わせの理
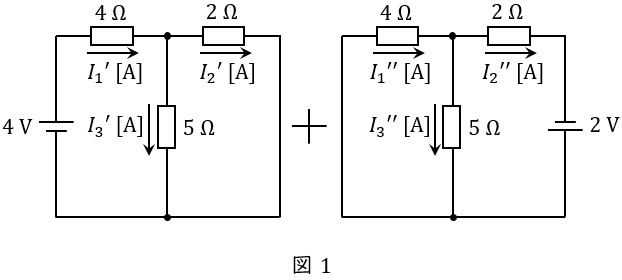
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。本問において回路は図1のように分解できます。
2.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.分圧・分流の法則
①分圧の法則
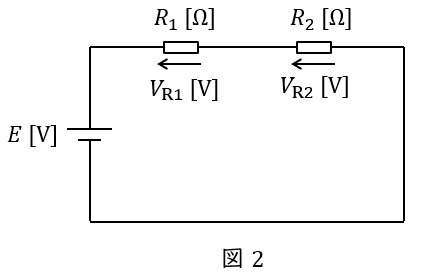
図2に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]
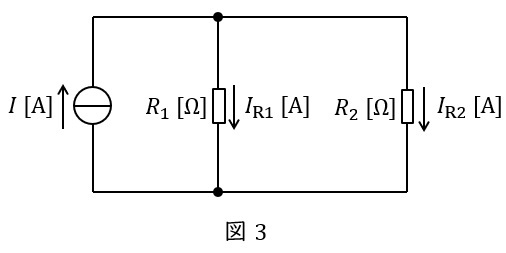
②分流の法則
図3に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
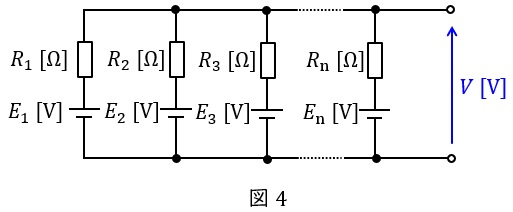
4.ミルマンの定理
図4のような,電源\( \ E_{1} \ \mathrm {[V]} \ \),\( \ E_{2} \ \mathrm {[V]} \ \),\( \ \cdots \ \),\( \ E_{\mathrm {n}} \ \mathrm {[V]} \ \)と抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \),\( \ R_{2} \ \mathrm {[\Omega ]} \ \),\( \ \cdots \ \),\( \ R_{\mathrm {n}} \ \mathrm {[\Omega ]} \ \)が直並列された回路における全体の電圧\( \ V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}+\frac {E_{3}}{R_{3}}+\cdots +\frac {E_{\mathrm {n}}}{R_{\mathrm {n}}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}+\cdots +\frac {1}{R_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。電源が繋がっていない場合は\( \ E=0 \ \mathrm {[V]} \ \),電源が逆向きの場合は\( \ -E \ \mathrm {[V]} \ \)とすればミルマンの定理はそのまま適用できます。
【解答】
解答:(3)
問題図に重ね合わせの理を適用すると図1のようになる。
図1左における回路の合成抵抗\( \ R^{\prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R^{\prime }&=&4+\frac {2\times 5}{2+5} \\[ 5pt ]
&≒&5.429 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,\( \ {I_{1}}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{I_{1}}^{\prime }&=&\frac {4}{R^{\prime }} \\[ 5pt ]
&=&\frac {4}{5.429} \\[ 5pt ]
&≒&0.736 \ 8 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって分流の法則より,\( \ {I_{2}}^{\prime } \ \mathrm {[A]} \ \)及び\( \ {I_{3}}^{\prime } \ \mathrm {[A]} \ \)は,ワンポイント解説「3.分圧・分流の法則」の通り,
\[
\begin{eqnarray}
{I_{2}}^{\prime }&=&\frac {5}{2+5} {I_{1}}^{\prime } \\[ 5pt ]
&=&\frac {5}{2+5} \times 0.736 \ 8 \\[ 5pt ]
&≒&0.526 \ 3 \ \mathrm {[A]} \\[ 5pt ]
{I_{3}}^{\prime }&=&\frac {2}{2+5} {I_{1}}^{\prime } \\[ 5pt ]
&=&\frac {2}{2+5} \times 0.736 \ 8 \\[ 5pt ]
&≒&0.210 \ 5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
同様に,図1右における回路の合成抵抗\( \ R^{\prime \prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R^{\prime \prime }&=&2+\frac {4\times 5}{4+5} \\[ 5pt ]
&≒&4.222 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,\( \ {I_{2}}^{\prime \prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{I_{2}}^{\prime \prime }&=&\frac {2}{R^{\prime \prime }} \\[ 5pt ]
&=&\frac {2}{4.222} \\[ 5pt ]
&≒&0.473 \ 7 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって分流の法則より,\( \ {I_{1}}^{\prime \prime } \ \mathrm {[A]} \ \)及び\( \ {I_{3}}^{\prime \prime } \ \mathrm {[A]} \ \)は,電流の向きに注意すると,
\[
\begin{eqnarray}
{I_{1}}^{\prime \prime }&=&\frac {5}{4+5} {I_{2}}^{\prime } \\[ 5pt ]
&=&\frac {5}{4+5} \times 0.473 \ 7 \\[ 5pt ]
&≒&0.263 \ 2 \ \mathrm {[A]} \\[ 5pt ]
{I_{3}}^{\prime \prime }&=&-\frac {4}{4+5} {I_{2}}^{\prime } \\[ 5pt ]
&=&-\frac {4}{4+5} \times 0.473 \ 7 \\[ 5pt ]
&≒&-0.210 \ 5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。以上から,各抵抗を流れる電流\( \ I_{1} \ \mathrm {[A]} \ \),\( \ I_{2} \ \mathrm {[A]} \ \),\( \ I_{3} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{I_{1}}&=&{I_{1}}^{\prime }+{I_{1}}^{\prime \prime } \\[ 5pt ]
&=&0.736 \ 8+0.263 \ 2 \\[ 5pt ]
&=&1.00 \ \mathrm {[A]} \\[ 5pt ]
{I_{2}}&=&{I_{2}}^{\prime }+{I_{2}}^{\prime \prime } \\[ 5pt ]
&=&0.526 \ 3+0.473 \ 7 \\[ 5pt ]
&=&1.00 \ \mathrm {[A]} \\[ 5pt ]
{I_{3}}&=&{I_{3}}^{\prime }+{I_{3}}^{\prime \prime } \\[ 5pt ]
&=&0.210 \ 5-0.210 \ 5 \\[ 5pt ]
&=&0.00 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
ミルマンの定理より,\( \ 5 \ \mathrm {\Omega } \ \)の抵抗に加わる電圧\( \ V_{3} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{3}&=&\frac {\displaystyle \frac {4}{4}-\frac {2}{2}+\frac {0}{5}}{\displaystyle \frac {1}{4}+\frac {1}{2}+\frac {1}{5}} \\[ 5pt ]
&=&0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 5 \ \mathrm {\Omega } \ \)の抵抗には電流が流れず\( \ I_{3}=0 \ \mathrm {[A]} \ \)と求められる。
これより,\( \ 5 \ \mathrm {\Omega } \ \)の抵抗は切り離して考えて良いから,回路は図5のようになる。したがって,各抵抗を流れる電流\( \ I_{1} \ \mathrm {[A]} \ \),\( \ I_{2} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{I_{1}}={I_{2}}&=&\frac {4+2}{4+2} \\[ 5pt ]
&=&1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは