《電力》〈配電〉[H20:問17]三相3線式配電線路の電圧降下に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

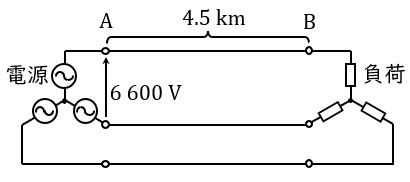
図のような三相高圧配電線路\( \ \mathrm {A-B} \ \)がある。\( \ \mathrm {B} \ \)点の負荷に電力を供給するとき，次の(a)及び(b)に答えよ。

ただし，配電線路の使用電線は硬銅より線で，その抵抗率は\( \ \displaystyle \frac {1}{55} \ \mathrm {[\Omega \cdot {mm}^{2}/m]} \ \)，線路の誘導性リアクタンスは無視するものとし，\( \ \mathrm {A} \ \)点の電圧は三相対称であり，その線間電圧は\( \ 6 \ 600 \ \mathrm {[V]} \ \)で一定とする。また，\( \ \mathrm {B} \ \)点の負荷は三相平衡負荷とし，一相当たりの負荷電流は\( \ 200 \ \mathrm {[A]} \ \)，力率\( \ 100 \ \mathrm {[％]} \ \)で一定とする。

(a)　配電線路の使用電線が各相とも硬銅より線の断面積が\( \ 60 \ \mathrm {[{mm}^{2}]} \ \)であったとき，負荷\( \ \mathrm {B} \ \)点における線間電圧\( \ \mathrm {[V]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 6 \ 055 \ \)　　(2)　\( \ 6 \ 128 \ \)　　(3)　\( \ 6 \ 205 \ \)　　(4)　\( \ 6 \ 297 \ \)　　(5)　\( \ 6 \ 327 \ \)

(b)　配電線路\( \ \mathrm {A-B} \ \)間の線間の電圧降下を\( \ 300 \ \mathrm {[V]} \ \)以内にすることができる電線の断面積\( \ \mathrm {[{mm}^{2}]} \ \)を次のうちから選ぶとすれば，最小のものはどれか。

ただし，電線は各相とも同じ断面積とする。

　(1)　\( \ 60 \ \)　　(2)　\( \ 80 \ \)　　(3)　\( \ 100 \ \)　　(4)　\( \ 120 \ \)　　(5)　\( \ 150 \ \)

【ワンポイント解説】

三相\( \ 3 \ \)線式配電線路における電圧降下を検討する問題です。
(a)も(b)も同じ公式を使用するため，理解している方は両方とも解ける点数差が開きやすい問題です。以下のワンポイント解説の内容はいずれも電験で出題されやすい内容なので，理解しておくようにして下さい。

1.抵抗率と導電率
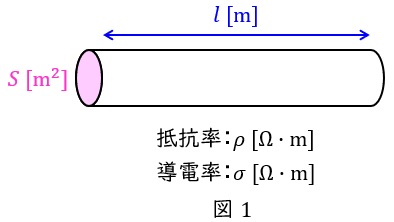
図1に示すように，導体の断面積\( \ 1 \ \mathrm {m^{2}} \ \)，長さ\( \ 1 \ \mathrm {m} \ \)あたりの抵抗率（導体材料の電流の流れにくさ）が\( \ \rho \ \mathrm {[\Omega \cdot m ]} \ \)，抵抗率の逆数である導電率（導体材料の電流の流れやすさ）が\( \ \sigma \ \mathrm {[S/m ]} \ \)であるとき，断面積\( \ S \ \mathrm {[m^{2}]} \ \)，長さ\( \ l \ \mathrm {[m]} \ \)の導体の抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S}=\frac {l}{\sigma S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式
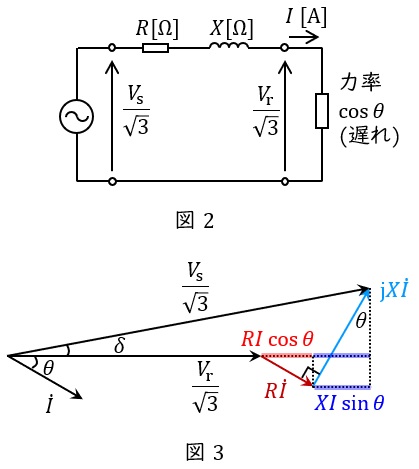
三相回路においては，一相分の等価回路及びベクトル図は図2及び図3のように描くことができ，送電端電圧と受電端電圧の位相差\( \ \delta \ \mathrm {[rad]} \ \)が無視できるぐらい小さいとしたときの電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] \frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(2)
送電線の抵抗率が\( \ \rho =\displaystyle \frac {1}{55} \ \mathrm {[\Omega \cdot {mm}^{2}/m]} \ \)，断面積が\( \ S=60 \ \mathrm {[{mm}^{2}]} \ \)，長さが\( \ l=4 \ 500 \ \mathrm {[m]} \ \)なので，抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.抵抗率と導電率」の通り，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{55}\times 4 \ 500}{60} \\[ 5pt ] &≒&1.364 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，配電線での電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，負荷電流\( \ I=200 \ \mathrm {[A]} \ \)，リアクタンス分が無視できるため力率\( \ \cos \theta =1 \ \)であるから，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] &=&\sqrt {3}\times 200 \times \left( 1.364 \times 1 +0\times 0 \right) \\[ 5pt ] &≒&472.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ \mathrm {A} \ \)点の線間電圧\( \ V_{\mathrm {A}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，\( \ \mathrm {B} \ \)点の線間電圧\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&V_{\mathrm {A}}-\varepsilon \\[ 5pt ] &=&6 \ 600-472.5 \\[ 5pt ] &≒&6 \ 128 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
配電線路の電圧降下を\( \ \varepsilon ^{\prime }=300 \ \mathrm {[V]} \ \)以内にするための送電線の許容抵抗値\( \ R^{\prime } \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&\sqrt {3}I\left( R^{\prime }\cos \theta +X\sin \theta \right) \\[ 5pt ] &=&\sqrt {3}IR^{\prime } \\[ 5pt ] R^{\prime }&=&\frac {\varepsilon ^{\prime }}{\sqrt {3}I} \\[ 5pt ] &=&\frac {300}{\sqrt {3}\times 200} \\[ 5pt ] &≒&0.8660 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，必要な電線の断面積\( \ S^{\prime } \ \mathrm {[{mm}^{2}]} \ \)は，ワンポイント解説「1.抵抗率と導電率」の通り，
\[
\begin{eqnarray}
R^{\prime } &=&\frac {\rho l}{S^{\prime }} \\[ 5pt ] S^{\prime } &=&\frac {\rho l}{R^{\prime }} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{55}\times 4 \ 500}{0.8660} \\[ 5pt ] &≒&94.5 \ \mathrm {[{mm}^{2}]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，選択肢のうち最小のものは\( \ 100 \ \mathrm {{mm}^{2}} \ \)と求められる。