Contents
【問題】
【難易度】★★★☆☆(普通)
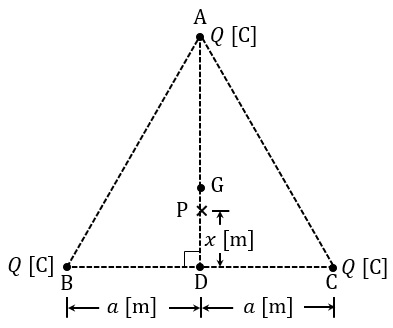
真空中において,図のように一辺が\( \ 2a \ \mathrm {[m]} \ \)の正三角形の各頂点\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)に正の点電荷\( \ Q \ \mathrm {[C]} \ \)が配置されている,点\( \ \mathrm {A} \ \)から辺\( \ \mathrm {BC} \ \)の中点\( \ \mathrm {D} \ \)に下ろした垂線上の点\( \ \mathrm {G} \ \)を正三角形の重心とする。点\( \ \mathrm {D} \ \)から \( \ x \ \mathrm {[m]} \ \)離れた点\( \ \mathrm {P} \ \)の電界\( \ \mathrm {[V / m]} \ \)の大きさを表わす式として,正しいのは次のうちどれか。
ただし,点\( \ \mathrm {P} \ \)は点\( \ \mathrm {D} \ \)と点\( \ \mathrm {G} \ \)間の垂線上にあるものとし,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とする。
\[
\begin{eqnarray}
&(1)& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{\left( \sqrt {3}a-x\right) }+\frac {2}{\sqrt {a^{2}+x^{2}}}\right] &(2)& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{\left( \sqrt {3}a-x\right) ^{2}}+\frac {2}{\left( a^{2}+x^{2}\right) }\right] \\[ 5pt ]
&(3)& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{\left( \sqrt {3}a-x\right) ^{2}}-\frac {2}{\left( a^{2}+x^{2}\right) }\right] &(4)& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{\left( \sqrt {3}a-x\right) ^{2}}+\frac {2x}{\left( a^{2}+x^{2}\right) ^{\frac {3}{2}}}\right] \\[ 5pt ]
&(5)& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{\left( \sqrt {3}a-x\right) ^{2}}-\frac {2x}{\left( a^{2}+x^{2}\right) ^{\frac {3}{2}}}\right] && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
複数の点電荷が正三角形の垂線上に及ぼす電界の大きさを導出する問題です。
用いる公式は少ないですが,三平方の定理等を駆使した計算力が問われる問題です。
1.真空中の電界の大きさ
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時,電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電界の大きさ\( \ E \ \mathrm {[N / C]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。この場所に電荷\( \ q \ \mathrm {[C]} \ \)の電荷を置けば,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
の力が働きます。
【解答】
解答:(5)
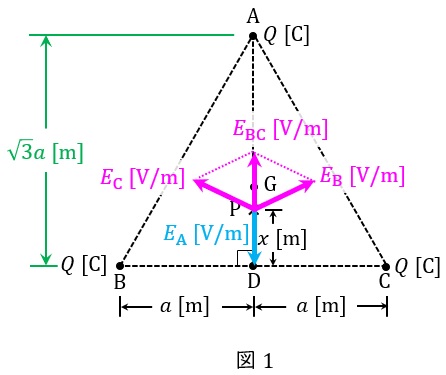
図1のように各点電荷による電界を\( \ E_{\mathrm {A}} \ \mathrm {[V / m]} \ \),\( \ E_{\mathrm {B}} \ \mathrm {[V / m]} \ \),\( \ E_{\mathrm {C}} \ \mathrm {[V / m]} \ \)とすると,それぞれの大きさは,ワンポイント解説「1.真空中の電界の大きさ」の通り,
\[
\begin{eqnarray}
E_{\mathrm {A}} &=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {3}a-x\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
E_{\mathrm {B}} =E_{\mathrm {C}}&=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {a^{2}+x^{2}}\right) ^{2}} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}\left( a^{2}+x^{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ E_{\mathrm {B}} \ \mathrm {[V / m]} \ \)と\( \ E_{\mathrm {C}} \ \mathrm {[V / m]} \ \)の合成電界\( \ E_{\mathrm {BC}} \ \mathrm {[V / m]} \ \)は,図の上向きとなり,
\[
\begin{eqnarray}
E_{\mathrm {BC}}&=&E_{\mathrm {B}}\times \frac {x}{\sqrt {a^{2}+x^{2}}}\times 2 \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}\left( a^{2}+x^{2}\right) }\times \frac {x}{\sqrt {a^{2}+x^{2}}}\times 2 \\[ 5pt ]
&=&\frac {2Qx}{4\pi \varepsilon _{0}\left( a^{2}+x^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,全体の合成電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
E&=&E_{\mathrm {A}}-E_{\mathrm {BC}} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {3}a-x\right) ^{2}}-\frac {2Qx}{4\pi \varepsilon _{0}\left( a^{2}+x^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}}\left\{ \frac {1}{\left( \sqrt {3}a-x\right) ^{2}}-\frac {2x}{\left( a^{2}+x^{2}\right) ^{\frac {3}{2}}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは