Contents
【問題】
【難易度】★★★☆☆(普通)
均等放射の球形光源(球の直径は\( \ 30 \ \mathrm {cm} \ \))がある。床からこの球形光源の中心までの高さは\( \ 3 \ \mathrm {m} \ \)である。また,球形光源から放射される全光束は\( \ 12 \ 000 \ \mathrm {lm} \ \)である。次の(a)及び(b)の問に答えよ。
(a) 球形光源直下の床の水平面照度の値\( \ \mathrm {[lx]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,天井や壁など,周囲からの反射光の影響はないものとする。
(1) \( \ 35 \ \) (2) \( \ 106 \ \) (3) \( \ 142 \ \) (4) \( \ 212 \ \) (5) \( \ 425 \ \)
(b) 球形光源の光度の値\( \ \mathrm {[cd]} \ \)と輝度の値\( \ \mathrm {[cd/m^{2}]} \ \)との組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 光度 & 輝度 \\
\hline
(1) & 955 & 13 \ 500 \\
\hline
(2) & 955 & 3 \ 380 \\
\hline
(3) & 1 \ 910 & 1 \ 010 \\
\hline
(4) & 1 \ 910 & 27 \ 000 \\
\hline
(5) & 3 \ 820 & 13 \ 500 \\
\hline
\end{array}
\]
【ワンポイント解説】
球形光源による水平面照度と球形光源の光度・輝度を求める問題です。
合格のためには(a)を間違えたくない問題となります。照度の問題は過去問でも何度も出題されていますので,必ず解けるようになりましょう。
本問は平成26年問17からの再出題となります。
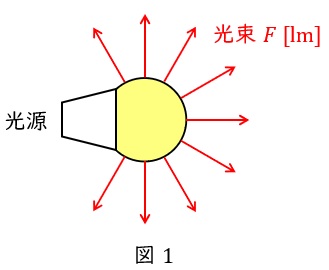
1.光束\( \ F \ \)
光源から出る可視光の量(エネルギー)で,単位は\( \ \mathrm {[lm]} \ \)となります。
電磁気の分野の電束に似たようなイメージで良いです。
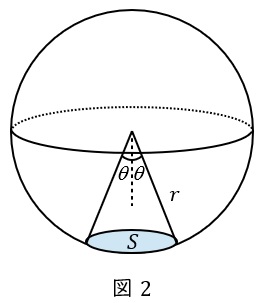
2.立体角の定義
図2のように球体があり,半径\( \ r \ \mathrm {[m]} \ \)の錐体が球面を切り取った時の面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると,立体角\( \ \omega \ \mathrm {[sr]} \ \)は,
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,平面角\( \ \theta \ \mathrm {[rad]} \ \)で表すと,
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。球全体の立体角は\( \ \theta = \pi \ \)の時であり,\( \ \omega =4\pi \ \)となります。
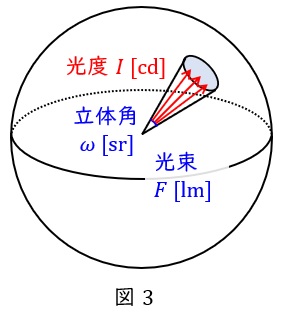
3.光度\( \ I \ \)
ある方向に向かう光束\( \ F \ \mathrm {[lm]} \ \)を立体角\( \ \omega \ \mathrm {[sr]} \ \)で割ったもので,光度\( \ I \ \mathrm {[cd]} \ \)を式で表すと,
\[
\begin{eqnarray}
I &=&\frac {F}{\omega } \\[ 5pt ]
\end{eqnarray}
\]
となります。
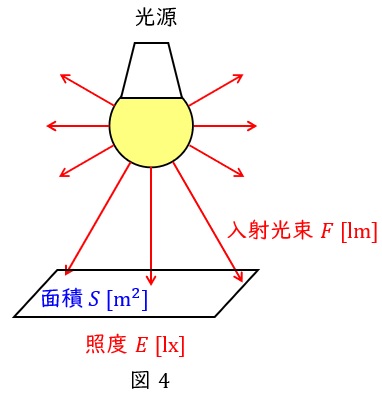
4.照度\( \ E \ \)
図4のように,面積\( \ S \ \mathrm {[m^{2}]} \ \)へ入射する光束が\( \ F \ \mathrm {[lm]} \ \ \)であるとき,平均照度\( \ E \ \mathrm {[lx]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ]
\end{eqnarray}
\]
となり,光源からある方向へ向かう光度が\( \ I \ \mathrm {[cd]} \ \)であるとき,光源からの距離\( \ l \ \mathrm {[m]} \ \)離れた垂直面の照度\( \ E \ \mathrm {[lx]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ]
&=&\frac {4\pi I}{4\pi l^{2}} \\[ 5pt ]
&=&\frac {I}{l^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。このように,一般に物理量が\( \ 2 \ \)乗に反比例する法則を逆\( \ 2 \ \)乗の法則といいます。
5.輝度\( \ L \ \)
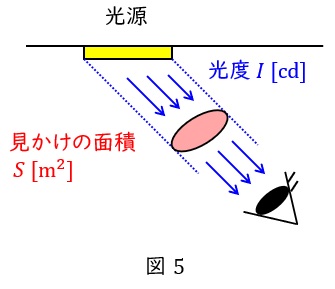
図5のように,ある方向から見た光源のまぶしさを表す指標で,光源からある方向へ向かう光度が\( \ I \ \mathrm {[cd]} \ \)であるとき,輝度\( \ L \ \mathrm {[cd/m^{2}]} \ \)は,同じ方向から照明を見た投影面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると,
\[
\begin{eqnarray}
L&=&\frac {I}{S} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(a)解答:(2)
均等放射の球形光源から床に向かう光度\( \ I \ \mathrm {[cd]} \ \)は,球形光源の全光束が\( \ F=12 \ 000 \ \mathrm {[lm]} \ \)であるから,ワンポイント解説「2.立体角の定義」及び「3.光度\( \ I \ \)」の通り,
\[
\begin{eqnarray}
I &=&\frac {F}{4\pi } \\[ 5pt ]
&=&\frac {12 \ 000}{4\pi } \\[ 5pt ]
&≒&954.9 \ \mathrm {[cd]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,球形光源の直下における水平面照度\( \ E \ \mathrm {[lx]} \ \)の大きさは,光源からの距離\( \ l=3 \ \mathrm {[m]} \ \)なので,ワンポイント解説「4.照度\( \ E \ \)」の通り,
\[
\begin{eqnarray}
E &=&\frac {I}{l^{2}} \\[ 5pt ]
&=&\frac {954.9}{3^{2}} \\[ 5pt ]
&=&106.1 → 106 \ \mathrm {[lx]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
(a)より,球形光源の光度\( \ I=954.9 \ → \ 955 \ \mathrm {[cd]} \ \)と求められる。
また,球形光源をみたときの投影面積\( \ S \ \mathrm {[m^{2}]} \ \)は,球形光源の直径が\( \ D=0.3 \ \mathrm {[m]} \ \)より,
\[
\begin{eqnarray}
S &=&\pi \left( \frac {D}{2}\right) ^{2} \\[ 5pt ]
&=&\pi \times \left( \frac {0.3}{2}\right) ^{2} \\[ 5pt ]
&≒&0.070 \ 69 \ \mathrm {[m^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,光源の輝度\( \ L \ \mathrm {[cd/m^{2}]} \ \)は,ワンポイント解説「5.輝度\( \ L \ \)」の通り,
\[
\begin{eqnarray}
L &=&\frac {I}{S} \\[ 5pt ]
&=&\frac {954.9}{0.070 \ 69} \\[ 5pt ]
&≒&13 \ 508 → 13 \ 500 \ \mathrm {[cd/m^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは