Contents
【問題】
【難易度】★★★☆☆(普通)
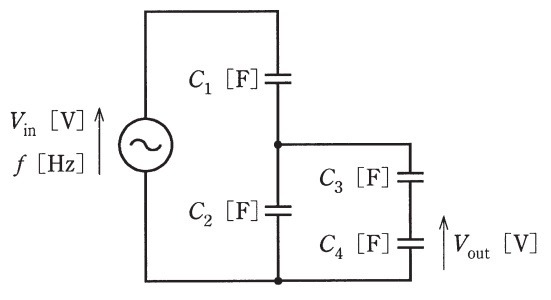
図のように,静電容量\(C_{1}=10 \ \mathrm{\mu F}\),\(C_{2}=900 \ \mathrm{\mu F}\),\(C_{3}=100 \ \mathrm{\mu F}\),\(C_{4}=900 \ \mathrm{\mu F}\)のコンデンサからなる直並列回路がある。この回路に周波数\(f=50 \ \mathrm{Hz}\)の交流電圧\(V_{\mathrm {in}} \ [ \mathrm {V} ]\)を加えたところ,\(C_{4}\)の両端の交流電圧は\(V_{\mathrm {out}} \ [ \mathrm {V} ]\)であった。
このとき,\(\displaystyle \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}\)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac {1}{1000}\) (2) \(\displaystyle \frac {9}{1000}\) (3) \(\displaystyle \frac {1}{100}\) (4) \(\displaystyle \frac {99}{100}\) (5) \(\displaystyle \frac {891}{1000}\)
【ワンポイント解説】
コンデンサのインピーダンスの分圧を計算できるかを問う問題です。静電容量が大きいほどインピーダンスが小さくなるという特徴を理解して下さい。
1.交流回路におけるコンデンサのインピーダンス
交流回路における,コンデンサのリアクタンス\(X \ [\Omega ]\)は,角周波数\(\omega \),周波数\(f\)とすると,
\[
\begin{eqnarray}
X&=&\frac {1}{\omega C} \\[ 5pt ]
&=&\frac {1}{2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
コンデンサ\(C_{3}\)と\(C_{4}\)の合成静電容量\(C_{34}\)は,
\[
\begin{eqnarray}
C_{34}&=&\frac {C_{3}C_{4}}{C_{3}+C_{4}} \\[ 5pt ]
&=&\frac {100\times 900}{100+900} \\[ 5pt ]
&=&90 \ \mathrm{[\mu F]} \\[ 5pt ]
\end{eqnarray}
\]
であり,コンデンサ\(C_{2}\)と\(C_{3}\),\(C_{4}\)の合成静電容量\(C_{234}\)は,
\[
\begin{eqnarray}
C_{234}&=&C_{2}+C_{34}\\[ 5pt ]
&=&900+90 \\[ 5pt ]
&=&990 \ \mathrm{[\mu F]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コンデンサ\(C_{2}\)の両端にかかる電圧\(V_{2}\)は,分圧の関係より,
\[
\begin{eqnarray}
V_{2}&=&\frac {\frac {1}{2\pi f C_{234}}}{\frac {1}{2\pi f C_{1}}+\frac {1}{2\pi f C_{234}}}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {\frac {1}{C_{234}}}{\frac {1}{C_{1}}+\frac {1}{C_{234}}}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {C_{1}}{C_{1}+C_{234}}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {10}{10+990}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {1}{100}V_{\mathrm {in}}
\end{eqnarray}
\]
となる。また,同様にコンデンサ\(C_{4}\)の両端にかかる電圧\(V_{4}\)は,分圧の関係より,
\[
\begin{eqnarray}
V_{4}&=&\frac {\frac {1}{2\pi f C_{4}}}{\frac {1}{2\pi f C_{3}}+\frac {1}{2\pi f C_{4}}}V_{2} \\[ 5pt ]
&=&\frac {\frac {1}{C_{4}}}{\frac {1}{C_{3}}+\frac {1}{C_{4}}}V_{2} \\[ 5pt ]
&=&\frac {C_{3}}{C_{3}+C_{4}}V_{2} \\[ 5pt ]
&=&\frac {100}{100+900}\frac {1}{100}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {1}{1000}V_{\mathrm {in}}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは