《理論》〈電子理論〉[H29:問13]バイポーラトランジスタに関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

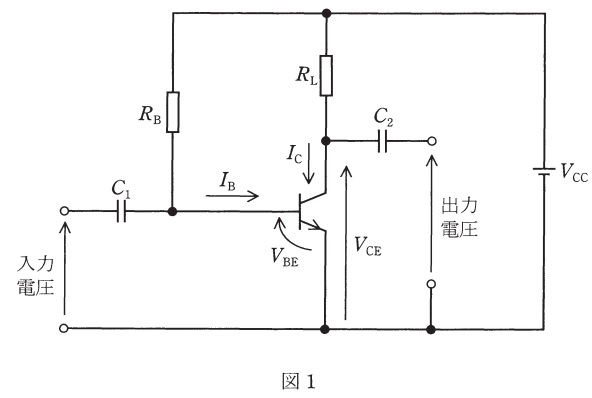
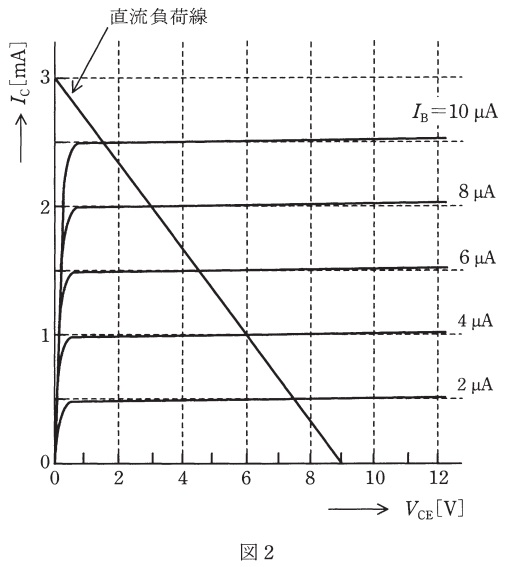
図1は，固定バイアス回路を用いたエミッタ接地トランジスタ増幅回路である。図2は，トランジスタの五つのベース電流\( \ I_{\mathrm {B}} \ \)に対するコレクタ－エミッタ間電圧\( \ V_{\mathrm {CE}} \ \)とコレクタ電流\( \ I_{\mathrm {C}} \ \)との静特性を示している。この\( \ V_{\mathrm {CE}}-I_{\mathrm {C}} \ \)特性と直流負荷線との交点を動作点という。図1の回路の直流負荷線は図2のように与えられる。動作点が\( \ V_{\mathrm {CE}}=4.5 \ \mathrm {V} \ \)のとき，バイアス抵抗\( \ R_{\mathrm {B}} \ \)の値\( \ \mathrm {\left[ M\Omega\right] } \ \)として最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，ベース－エミッタ間電圧\( \ V_{\mathrm {BE}} \ \)は，直流電源電圧\( \ V_{\mathrm {CC}} \ \)に比べて十分小さく無視できるものとする。なお，\( \ R_{\mathrm {L}} \ \)は負荷抵抗であり，\( \ C_{1} \ \)，\( \ C_{2} \ \)は結合コンデンサである。

(1)　\(0.5\)　　(2)　\(1.0\)　　(3)　\(1.5\)　　(4)　\(3.0\)　　(5)　\(6.0\)

【ワンポイント解説】

典型的な電子回路の計算問題ですが，途中の計算過程のヒントがなく，\( \ R_{\mathrm {B}} \ \)を一気に求めさせようとしているので，やや難しい問題と言えます。本問は今後，類題も出題される可能性があるため，よく理解しておきましょう。

【解答】

解答：(3)
本問は以下の2ステップに分けて説明します。

①\( \ V_{\mathrm {CC}} \ \)の導出
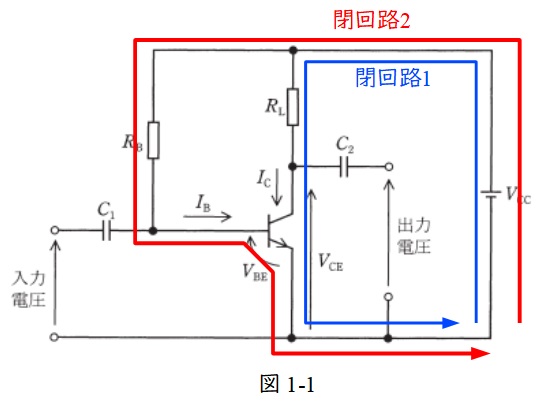
図1-1の閉回路1について考える。
閉回路1において，キルヒホッフの法則より，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&V_{\mathrm {CE}}+R_{\mathrm {L}}I_{\mathrm {C}} \\[ 5pt ] \end{eqnarray}
\] が成り立つ。ここで，図2から\( \ I_{\mathrm {C}}=0 \ \mathrm {A} \ \)の時，\( \ V_{\mathrm {CE}}=9 \ \mathrm {V} \ \)であるから，これを上式に代入すると，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&9+R_{\mathrm {L}}\times 0 \\[ 5pt ] &=&9 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] が求められる。

②\( \ R_{\mathrm {B}} \ \)の導出
図1-1の閉回路2について考える。
閉回路2において，キルヒホッフの法則から，
\[
V_{\mathrm {CC}}=R_{\mathrm {B}}I_{\mathrm {B}}+V_{\mathrm {BE}}
\] となる。題意より，\(V_{\mathrm {BE}}\)の大きさは無視できるので，
\[
V_{\mathrm {CC}}=R_{\mathrm {B}}I_{\mathrm {B}}
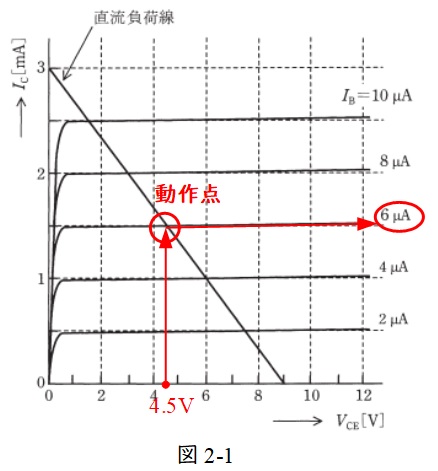
\] となる。ここで，動作点が\(V_{\mathrm {CE}}=4.5 \ \mathrm {V}\)であるから，図2-1の通り，この時のベース電流\(I_{\mathrm {B}}\)は\(6 \ \mathrm {\mu A}\)となる。これを上式に代入すると，
\[
\begin{eqnarray}
9&=&R_{\mathrm {B}}\times 6\times 10^{-6} \\[ 5pt ] R_{\mathrm {B}}&=&1.5\times 10^{6}\mathrm {[\Omega ]}　→　1.5 \ \mathrm {[M\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。