《理論》〈電気回路〉[H27:問8]交流回路の有効電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

\(R=10 \ \Omega \)の抵抗と誘導性リアクタンス\(X \ [ \Omega ] \)のコイルとを直列に接続し，\(100 \ \mathrm {V}\)の交流電源に接続した交流回路がある。いま，回路に流れる電流の値は\(I=5 \ \mathrm {A}\)であった。このとき，回路の有効電力\(P\)の値\(\mathrm {[ W ]} \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(250\)　　(2)　\(289\)　　(3)　\(425\)　　(4)　\(500\)　　(5)　\(577\)

【ワンポイント解説】

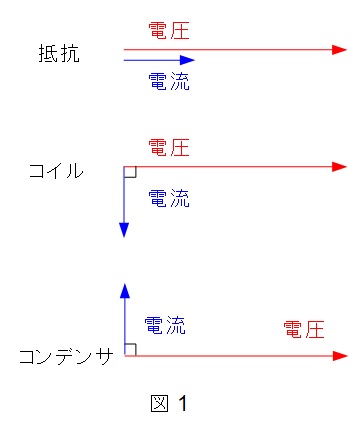
交流回路において，抵抗\(R\)とコイル等の誘導性リアクタンス\(X_{\mathrm {L}}\)，コンデンサ等の容量性リアクタンス\(X_{\mathrm {C}}\)の特性は非常に重要な内容です。下記の特性についてはよく理解しておきましょう。

1.交流回路における各インピーダンスの諸特性
①抵抗\(R\)
　電圧\(V\)と電流\(I\)の位相差はなく，
\[
I=\frac {V}{R}
\] 　となります。

②コイル\(X_{\mathrm {L}}=\omega L\)
　電流\(I\)は電圧\(V\)から\(\displaystyle \frac {\pi }{2} [\mathrm {rad}]\)遅れ，
\[
I=\frac {V}{X_{\mathrm {L}}}=\frac {V}{\omega L}
\] 　となります。

③コンデンサ\(\displaystyle X_{\mathrm {C}}=\frac {1}{\omega C}\)
　　電流\(I\)は電圧\(V\)から\(\displaystyle \frac {\pi }{2} [\mathrm {rad}]\)進み，
\[
I=\frac {V}{X_{\mathrm {C}}}=\omega CV
\] 　となります。

【解答】

解答：(1)
題意に沿って，回路図を描くと図2のようになり，さらに各インピーダンスの特性に注意してベクトル図を描くと図3のようになる。

　　

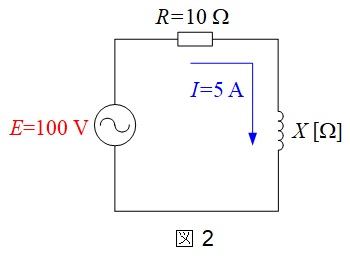
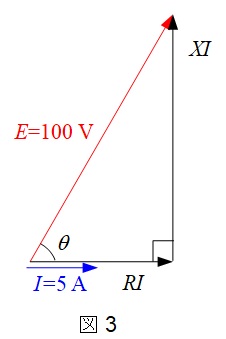
図3より，
\[
E=\sqrt {\left( RI \right) ^{2} +\left( XI \right) ^{2}}
\] となるから，各値を代入して整理すると，
\[
\begin{eqnarray}
E&=&\sqrt {\left( RI \right) ^{2} +\left( XI \right) ^{2}} \\[ 5pt ] E^{2}&=&\left( RI \right) ^{2} +\left( XI \right) ^{2} \\[ 5pt ] 100^{2}&=&\left( 10\times 5 \right) ^{2} +\left( X\times 5 \right) ^{2} \\[ 5pt ] 10000&=&2500 +25X^{2} \\[ 5pt ] 25X^{2}&=&7500 \\[ 5pt ] X^{2}&=&300 \\[ 5pt ] X&=&10\sqrt {3} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\(RI:XI=1:\sqrt {3}\)となるので，\(\displaystyle \theta =\frac {\pi}{3}\)となる。
したがって，回路の有効電力\(P\)は，
\[
\begin{eqnarray}
P&=&EI\cos \theta \\[ 5pt ] &=&100 \times 5 \times \cos \frac {\pi}{3} \\[ 5pt ] &=&250 \mathrm {[W]}
\end{eqnarray}
\] と求められる。

【別解】
回路で消費される有効電力は抵抗で消費される電力であるから，
\[
\begin{eqnarray}
P&=&RI^{2} \\[ 5pt ] &=&10\times 5^{2} \\[ 5pt ] &=&250 \mathrm {[W]}
\end{eqnarray}
\] と求められる。

※こちらの方がエレガントな解き方と言えますが，本ページではリアクタンスの諸特性についても説明したかったので，敢えてベクトル図を描いて解いています。