《法規》〈電気施設管理〉[R06下:問11]流込式水力発電所の年間可能発電電力量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

最大使用水量\( \ 15 \ \mathrm {m^{3} / s} \ \)，有効落差\( \ 20 \ \mathrm {m} \ \)の流込式水力発電所がある。

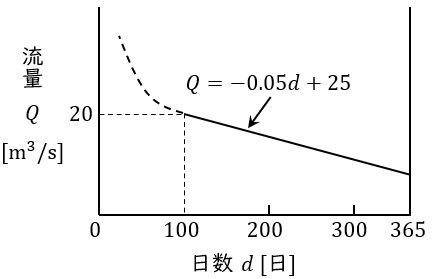
この発電所が利用している河川の流量\( \ Q \ \)が図のような年間流況曲線（日数\( \ d \ \)が\( \ 100 \ \)日以上の部分は，\( \ Q=-0.05d+25 \ \mathrm{[m^{3} / s]} \ \)で表される。）であるとき，次の(a)及び(b)の問に答えよ。ただし，水車及び発電機の効率はそれぞれ\( \ 90 \ \mathrm {％} \ \)及び\( \ 95 \ \mathrm {％} \ \)で，流量によって変化しないものとする。

(a)　この発電所で年間に溢水（いっすい）が発生する日数の合計として，最も近いのは次のうちどれか。
　　ただし，溢水とは河川流量を発電に利用しないで無効に放流することをいう。

　(1)　\( \ 180 \ \)　　(2)　\( \ 190 \ \)　　(3)　\( \ 200 \ \)　　(4)　\( \ 210 \ \)　　(5)　\( \ 220 \ \)

(b)　この発電所の年間可能発電電力量\( \ \mathrm {[GW\cdot h]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 19.3 \ \)　　(2)　\( \ 20.3 \ \)　　(3)　\( \ 21.4 \ \)　　(4)　\( \ 22.0 \ \)　　(5)　\( \ 22.5 \ \)

【ワンポイント解説】

流込式水力発電所の設計に関する問題です。
もちろん数学が得意な方は完答可能ですが，(b)で迷う受験生が多かったかと思います。合格のためには(a)を絶対に間違えないことが重要です。
本問はやや古いですが，平成15年問13からの再出題となります。

1.水力発電所の出力\( \ P \ \)
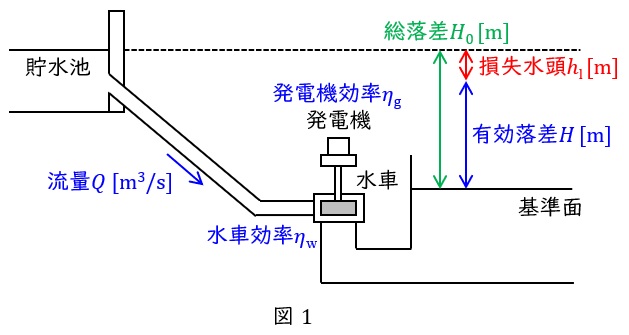
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}} \ \)，発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると，発電機の出力\( \ P \ \mathrm {[kW]} \ \)は
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m／s^{2}]} \ \)及び水の密度\( \ \rho =1 \ 000 \ \mathrm {[kg／m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] に各値を代入し，
\[
\begin{eqnarray}
P &=&1 \ 000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] &=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] として導出したものです。

【解答】

(a)解答：(3)
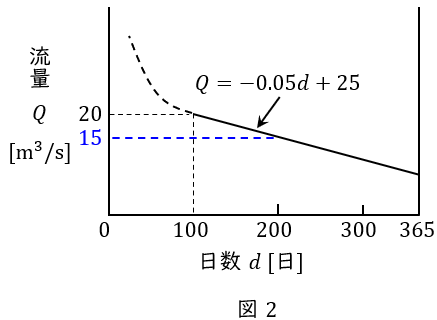
最大使用水量\( \ Q_{\mathrm {m}}=15 \ \mathrm {[m^{3} / s]} \ \)であるので，溢水が発生する日数\( \ d_{1} \ \mathrm {[日]} \ \)は図2より，
\[
\begin{eqnarray}
Q_{\mathrm {m}} &=&-0.05d_{1}+25 \\[ 5pt ] 15 &=&-0.05d_{1}+25 \\[ 5pt ] 0.05d_{1} &=&10 \\[ 5pt ] d_{1} &=&200 \ \mathrm {[日]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
最大使用水量\( \ Q_{\mathrm {m}}=15 \ \mathrm {[m^{3} / s]} \ \)のときの発電電力\( \ P_{1} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り，
\[
\begin{eqnarray}
P_{1} &=&9.8Q_{\mathrm {m}}H\eta _{\mathrm {w}}\eta _{\mathrm {g}} \\[ 5pt ] &=&9.8\times 15\times 20\times 0.90\times 0.95 \\[ 5pt ] &≒&2 \ 514 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
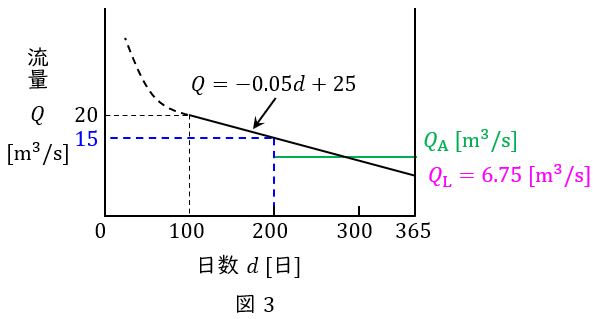
\] である。\( \ d=365 \ \mathrm {[日]} \ \)のときの流量\( \ Q_{\mathrm {L}} \ \mathrm {[m^{3} / s]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {L}} &=&-0.05d+25 \\[ 5pt ] &=&-0.05\times 365+25 \\[ 5pt ] &=&6.75 \ \mathrm {[m^{3} / s]} \\[ 5pt ] \end{eqnarray}
\] であるから，図3に示す\( \ 200～365 \ \mathrm {[日]} \ \)の間の平均流量\( \ Q_{\mathrm {A}} \ \mathrm {[m^{3} / s]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {A}} &=&\frac {Q_{\mathrm {m}}+Q_{\mathrm {L}}}{2} \\[ 5pt ] &=&\frac {15+6.75}{2} \\[ 5pt ] &≒&10.88 \ \mathrm {[m^{3} / s]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ 200～365 \ \mathrm {[日]} \ \)の間の平均発電電力\( \ P_{2} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り，
\[
\begin{eqnarray}
P_{2} &=&9.8Q_{\mathrm {A}}H\eta _{\mathrm {w}}\eta _{\mathrm {g}} \\[ 5pt ] &=&9.8\times 10.88\times 20\times 0.90\times 0.95 \\[ 5pt ] &≒&1 \ 823 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，発電所の年間可能発電電力量\( \ W \ \mathrm {[GW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W &=&P_{1}\times 24 \times 200+P_{2}\times 24 \times \left( 365-200\right) \\[ 5pt ] &=&2 \ 514\times 24 \times 200+1 \ 823\times 24 \times \left( 365-200\right) \\[ 5pt ] &≒&19 \ 300 \ 000 \ \mathrm {[kW\cdot h]}　→　19.3 \ \mathrm {[GW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。