Contents
【問題】
【難易度】★☆☆☆☆(易しい)
水力発電所の理論水力\( \ P \ \)は位置エネルギーの式から\( \ P=\rho g QH \ \)と表される。ここで\( \ H \ \mathrm {[m]} \ \)は有効落差,\( \ Q \ \mathrm {[m^{3}/s]} \ \)は流量,\( \ g \ \)は重力加速度\( \ =9.8 \ \mathrm {m/s^{2}} \ \),\( \ \rho \ \)は水の密度\( \ =1 \ 000 \ \mathrm {kg/m^{3}} \ \)である。以下に理論水力\( \ P \ \)の単位を検証することとする。なお,\( \ \mathrm {Pa} \ \)は「パスカル」,\( \ \mathrm {N} \ \)は「ニュートン」,\( \ \mathrm {W} \ \)は「ワット」,\( \ \mathrm {J} \ \)は「ジュール」である。
\( \ P=\rho gQH \ \)の単位は,\( \ \rho \ \),\( \ g \ \),\( \ Q \ \),\( \ H \ \)の単位の積であるから,\( \ \mathrm{kg/m^{3}\cdot m/s^{2}\cdot m^{3}/s\cdot m} \ \)となる。これを変形すると,\( \ \fbox { (ア) } \ \cdot \mathrm{m/s} \ \)となるが,\( \ \fbox { (ア) } \ \)は力の単位\( \ \fbox { (イ) } \ \)と等しい。すなわち\( \ P=\rho g QH \ \)の単位は\( \ \fbox { (イ) }\cdot \mathrm{m/s} \ \)となる。ここで,\( \ \fbox { (イ) } \ \cdot \mathrm {m} \ \)は仕事(エネルギー)の単位である\( \ \fbox { (ウ) } \ \)と等しいことから\( \ P=\rho g QH \ \)の単位は\( \ \fbox { (ウ) } \ / \mathrm {s} \ \)と表せ,これは仕事率(動力)の単位である\( \ \fbox { (エ) } \ \)と等しい。ゆえに、理論水力\( \ P=\rho g QH \ \)の単位は\( \ \fbox { (エ) } \ \)となるが,重力加速度\( \ g=9.8 \ \mathrm {m/s^{2}} \ \)と水の密度\( \ \rho =1 \ 000 \ \mathrm {kg/m^{3}} \ \)の数値\( \ 9.8 \ \)と\( \ 1 \ 000 \ \)を考慮すると,\( \ P=9.8QH \ [ \ \fbox { (オ) } \ ] \ \)と表せる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\[ 5pt ]
\hline
(1) & \mathrm {kg\cdot m} & \mathrm {Pa} & \mathrm {W} & \mathrm {J} & \mathrm {kJ} \\[ 5pt ]
\hline
(2) & \mathrm {kg\cdot m / s^{2}} & \mathrm {Pa} & \mathrm {J} & \mathrm {W} & \mathrm {kW} \\[ 5pt ]
\hline
(3) & \mathrm {kg\cdot m} & \mathrm {N} & \mathrm {J} & \mathrm {W} & \mathrm {kW} \\[ 5pt ]
\hline
(4) & \mathrm {kg\cdot m / s^{2}} & \mathrm {N} & \mathrm {W} & \mathrm {J} & \mathrm {kJ} \\[ 5pt ]
\hline
(5) & \mathrm {kg\cdot m / s^{2}} & \mathrm {N} & \mathrm {J} & \mathrm {W} & \mathrm {kW} \\[ 5pt ]
\hline
\end{array}
\]
【ワンポイント解説】
水力発電所の理論出力の導出に関する問題です。
様々な組立単位(\( \ \mathrm {[N]} \ \),\( \ \mathrm {[J]} \ \),\( \ \mathrm {[W]} \ \)等)を基本単位(\( \ \mathrm {[kg]} \ \),\( \ \mathrm {[m]} \ \),\( \ \mathrm {[s]} \ \)等)で表すことは,公式の定着にも繋がりとてもいい学習です。公式の丸暗記は良くない(ただし,必要な場合もあります。)ので,なぜその公式になるのかを理解しながら勉強すると良いと思います。
1.主な量記号の基本単位での表記
物理学で使用される\( \ \mathrm {SI} \ \)単位は基本単位として,\( \ \mathrm {[kg]} \ \),\( \ \mathrm {[m]} \ \),\( \ \mathrm {[s]} \ \),\( \ \mathrm {[A]} \ \),\( \ \mathrm {[mol]} \ \)等があり,さまざまな量記号は以下のように基本単位を用いて表すことができます。
①力\( \ F \ \mathrm {[N]} \ \)
運動方程式
\[
\begin{eqnarray}
F \ \mathrm {[N]}&=&m \ \mathrm {[kg]} \ a \ \mathrm {[m/s^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
より,
\[
\begin{eqnarray}
\mathrm {[N]}&=&\mathrm {[kg\cdot m/s^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②仕事\( \ W \ \mathrm {[J]} \ \)
仕事の定義式
\[
\begin{eqnarray}
W \ \mathrm {[J]}&=&F \ \mathrm {[N]} \ l \ \mathrm {[m]} \\[ 5pt ]
\end{eqnarray}
\]
より,
\[
\begin{eqnarray}
\mathrm {[J]}&=&\mathrm {[N\cdot m]}=\mathrm {[kg\cdot m^{2}/s^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
③仕事率あるいは電力\( \ P \ \mathrm {[W]} \ \)
仕事率の定義式
\[
\begin{eqnarray}
P \ \mathrm {[W]}&=&\frac {W \ \mathrm {[J]}}{t \ \mathrm {[s]}} \\[ 5pt ]
\end{eqnarray}
\]
より,
\[
\begin{eqnarray}
\mathrm {[W]}&=&\mathrm {[J/s]}=\mathrm {[kg\cdot m^{2}/s^{3}]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.水力発電所の出力\( \ P \ \)
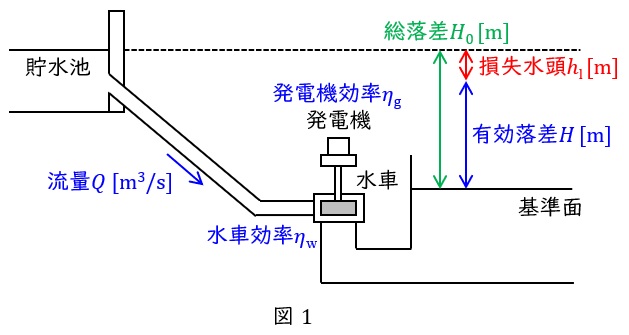
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}/s]} \ \),有効落差\( \ H \ \mathrm {[m]} \ \),水車効率\( \ \eta _{\mathrm {w}} \ \),発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると,発電機の出力\( \ P \ \mathrm {[kW]} \ \)は
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m/s^{2}]} \ \)及び水の密度\( \ \rho =1 \ 000 \ \mathrm {[kg/m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
に各値を代入し,
\[
\begin{eqnarray}
P &=&1 \ 000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
&=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
として導出したものです。
【解答】
解答:(5)
(ア)
理論水力\( \ P \ \)の単位は,
\[
\begin{eqnarray}
\mathrm{kg/m^{3}\cdot m/s^{2}\cdot m^{3}/s\cdot m}&=&\mathrm {kg\cdot m^{2}/s^{3}} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,題意に沿って変形すると,
\[
\begin{eqnarray}
\mathrm{kg\cdot m^{2}/s^{3}}&=&\mathrm{kg\cdot m/s^{2}\cdot m/s} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(イ)
ワンポイント解説「1.主な量記号の基本単位での表記」の通り,力の単位は\( \ \mathrm{[kg\cdot m/s^{2} ]=[N]} \ \)となります。
(ウ)
ワンポイント解説「1.主な量記号の基本単位での表記」の通り,仕事(エネルギー)の単位は\( \ \mathrm{[N\cdot m] =[J]} \ \)となります。
(エ)
ワンポイント解説「1.主な量記号の基本単位での表記」の通り,仕事率(動力)の単位は\( \ \mathrm{[J / s] =[W]} \ \)となります。
(オ)
ワンポイント解説「2.水力発電所の出力\( \ P \ \)」の通り,\( \ P=\rho gQH \ \)に\( \ g=9.8 \ \mathrm {[m/s^{2}]} \ \)と\( \ \rho =1 \ 000 \ \mathrm {[kg/m^{3}]} \ \)を代入すると,
\[
\begin{eqnarray}
P&=&1 \ 000\times 9.8 QH \ \mathrm {[W]}\\[ 5pt ]
&=&9.8 QH \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは