《電力》〈送電〉[R01:問13]支線に加わる送電線の張力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

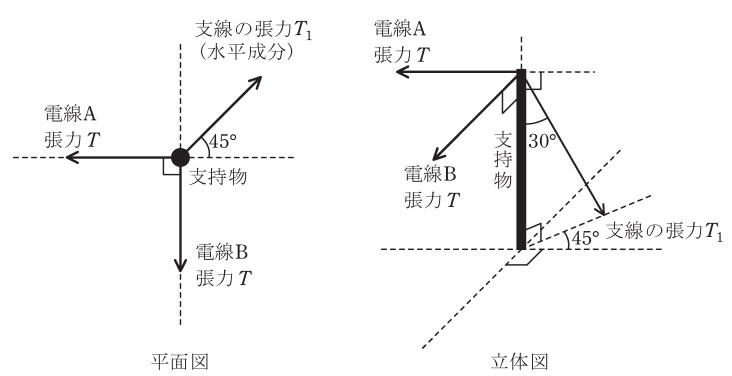
図に示すように，電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)の張力を，支持物を介して支線で受けている。電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)の張力の大きさは等しく，その値を\( \ T \ \)とする。支線に加わる張力\( \ T_{1} \ \)は電線張力\( \ T \ \)の何倍か。最も近いものを次の(1)～(5)のうちから一つ選べ。

なお，支持物は地面に垂直に立てられており，各電線は支線の取付け高さと同じ高さに取付けられている。また，電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)は地面に水平に張られているものとし，電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び支線の自重は無視する。

　(1)　\(\displaystyle \frac {1}{2}\)　　(2)　\(\displaystyle \frac {\sqrt {2}}{2}\)　　(3)　\(\sqrt {2}\)　　(4)　\(2\)　　(5)　\(2\sqrt {2}\)　　

【ワンポイント解説】

張力に関する問題で，電験では少し毛色の異なる分野の問題となります。力学の知識を必要としますが，比較的イメージしやすい内容となりますので，確実に理解しておくようにして下さい。

【解答】

解答：(5)
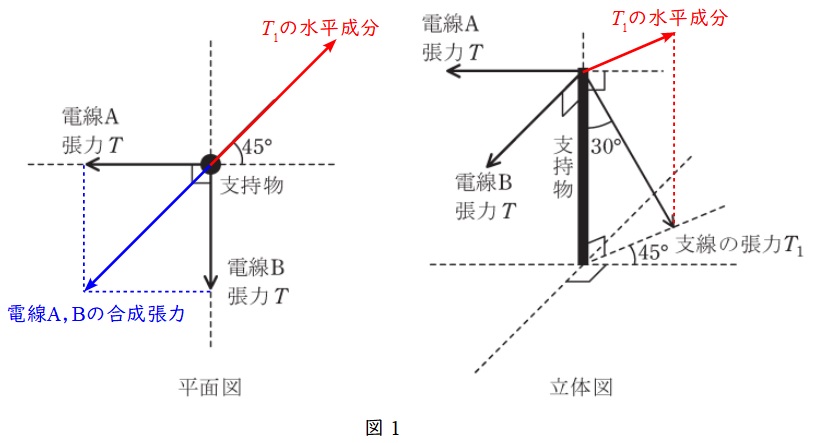
各図の力のベクトル図を書くと図1のようになる。図1より，電線の\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)の合成張力\( \ T_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
T_{\mathrm {C}}&=&\sqrt {T^{2}+T^{2}} \\[ 5pt ] &=&\sqrt {2}T \\[ 5pt ] \end{eqnarray}
\] であり，支線の張力\( \ T_{\mathrm {1}} \ \)の水平成分\( \ T_{\mathrm {1h}} \ \)は，
\[
\begin{eqnarray}
T_{\mathrm {1h}}&=&T_{\mathrm {1}}\sin 30° \\[ 5pt ] &=&\frac {T_{\mathrm {1}}}{2} \\[ 5pt ] \end{eqnarray}
\] である。両者が釣り合う必要があるから，
\[
\begin{eqnarray}
T_{\mathrm {C}}&=&T_{\mathrm {1h}} \\[ 5pt ] \sqrt {2}T&=&\frac {T_{\mathrm {1}}}{2} \\[ 5pt ] T_{\mathrm {1}}&=&2\sqrt {2}T \\[ 5pt ] \end{eqnarray}
\] と求められる。