《電力》〈配電〉[H19:問12]三相短絡事故が発生した時の短絡電流に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

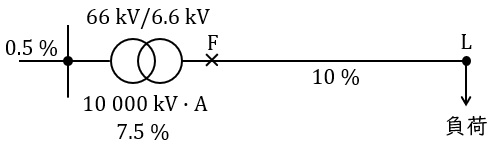
図のような三相\( \ 3 \ \)線式配電系統がある。配電用変電所の変圧器容量は\( \ 10 \ 000 \ \mathrm {[kV\cdot A]} \ \)，変圧比は\( \ 66 \ \mathrm {[kV]} / 6.6 \ \mathrm {[kV]} \ \)，百分率リアクタンスは自己容量基準で\( \ 7.5 \ \mathrm {[％]} \ \)であり，配電用変電所より上位系統側の百分率インピーダンスは基準容量\( \ 10 \ 000 \ \mathrm {[kV\cdot A]} \ \)で\( \ 0.5 \ \mathrm {[％]} \ \)とする。配電系統の末端\( \ \mathrm {L} \ \)点には負荷（抵抗負荷とする）が接続されており，配電用変電所の引出口\( \ \mathrm {F} \ \)点から\( \ \mathrm {L} \ \)点までの百分率インピーダンスは基準容量\( \ 10 \ 000 \ \mathrm {[kV\cdot A]} \ \)で\( \ 10 \ \mathrm {[％]} \ \)とする。\( \ \mathrm {F} \ \)点において三相完全短絡事故が発生したとき，\( \ \mathrm {F} \ \)点における短絡電流\( \ \mathrm {[kA]} \ \)の値として，最も近いのは次のうちどれか。
ただし，百分率インピーダンスは抵抗分を無視するものとする。

　(1)　\( \ 4.9 \ \)　　(2)　\( \ 8.7 \ \)　　(3)　\( \ 10.9 \ \)　　(4)　\( \ 11.7 \ \)　　(5)　\( \ 12.5 \ \)

【ワンポイント解説】

配電線路の三相短絡電流を求める問題です。
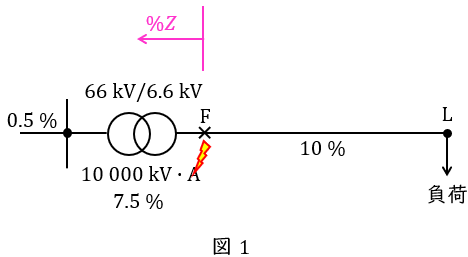
電験では電力科目だけではなく法規科目でも出題されやすい問題です。事故点より負荷側のインピーダンスは関係がない，すなわち本問においては余計な情報が与えられていることに注意して下さい。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 　(定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの短絡電流計算
ある地点から電源側を見た百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，その点での三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(3)
変圧器二次側の定格電流\( \ I_{n} \ \mathrm {[A]} \ \)は，基準容量\( \ P_{n}=10 \ 000 \ \mathrm {[kV\cdot A]} \ \)，基準電圧\( \ V_{n}=6.6 \ \mathrm {[kV]} \ \)より，
\[
\begin{eqnarray}
I_{n}&=&\frac {P_{n}}{\sqrt {3}V_{n}} \\[ 5pt ] &=&\frac {10 \ 000\times 10^{3}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒&874.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，事故点から電源側を見た百分率インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&0.5+7.5 \\[ 5pt ] &=&8.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であるから，三相短絡電流\( \ I_{s} \ \mathrm {[kA]} \ \)は，ワンポイント解説「2.百分率インピーダンスの短絡電流計算」の通り，
\[
\begin{eqnarray}
I_{s}&=&\frac {100I_{n}}{％Z} \\[ 5pt ] &=&\frac {100\times 874.8}{8.0} \\[ 5pt ] &≒&10 \ 900 \ \mathrm {[A]}　→　10.9 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。