《電力》〈変電〉[H19:問16]異容量 V 結線方式のベクトル図と過負荷にならない容量に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

\( \ 2 \ \)台の単相変圧器（容量\( \ 75 \ \mathrm {[kV\cdot A]} \ \)の\( \ \mathrm {T_{1}} \ \)及び容量\( \ 50 \ \mathrm {[kV\cdot A]} \ \)の\( \ \mathrm {T_{2}} \ \)）を\( \ \mathrm {V} \ \)結線に接続し，下図のように三相平衡負荷\( \ 45 \ \mathrm {[kW]} \ \)（力率角　進み\( \ \displaystyle \frac {\pi }{6} \ \mathrm {[rad]} \ \)）と単相負荷\( \ \mathrm {P} \ \)（力率\( \ =1 \ \)）に電力を供給している。これについて，次の(a)及び(b)に答えよ。

ただし，相順は\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)とし，図示していないインピーダンスは無視するものとする。

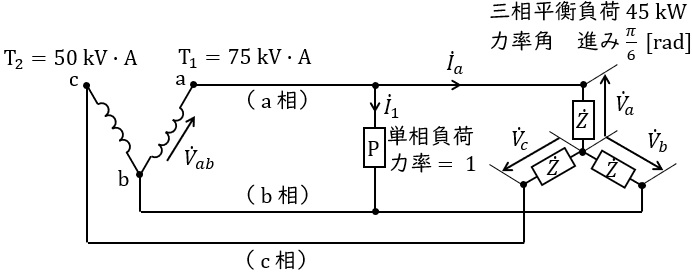
(a)　問題の図において，\( \ {\dot V}_{a} \ \)を基準とし，\( \ {\dot V}_{ab} \ \)，\( \ {\dot I}_{a} \ \)，\( \ {\dot I}_{1} \ \)の大きさと位相関係を表す図として，正しいのは次のうちどれか。
ただし，\( \ \left| {\dot I}_{a}\right| ＞ \left| {\dot I}_{1}\right| \ \)とする。

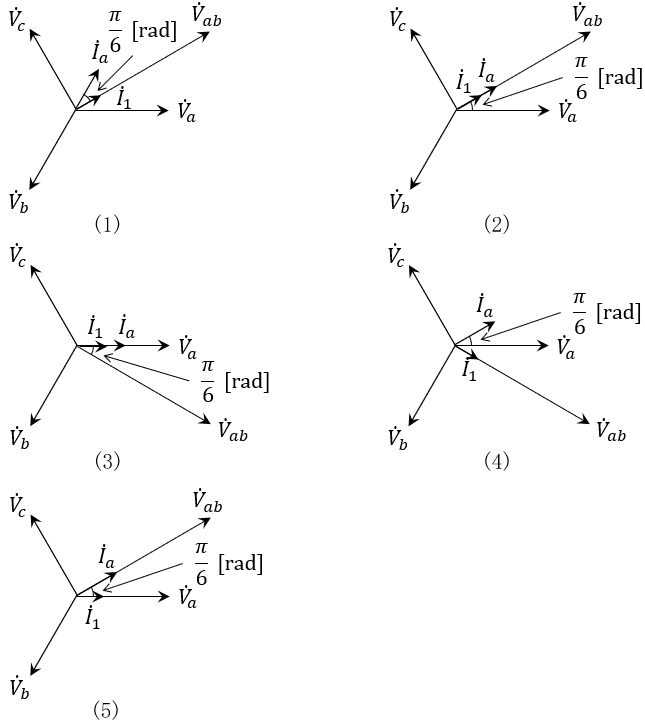
(b)　単相変圧器\( \ \mathrm {T_{1}} \ \)が過負荷にならない範囲で，単相負荷\( \ \mathrm {P} \ \)（力率\( \ =1 \ \)）がとりうる最大電力\( \ \mathrm {[kW]} \ \)の値として正しいのは次のうちどれか。

　(1)　\( \ 23 \ \)　　(2)　\( \ 36 \ \)　　(3)　\( \ 45 \ \)　　(4)　\( \ 49 \ \)　　(5)　\( \ 58 \ \)

【ワンポイント解説】

異容量\( \ \mathrm {V} \ \)結線方式の計算に関する問題です。
ベクトル図や力率，電力等の概念は理論科目で学習している前提での解説となりますので，わからないという方は理論科目のテキスト等を復習しておくようにして下さい。
設問(b)において，変圧器\( \ \mathrm {T_{2}} \ \)が過負荷となっているのが少し気になりますが，とりあえずは過負荷になっていないという前提で解いていくようにして下さい。

1.三相\( \ 4 \ \)線式異容量\( \ \mathrm {V} \ \)結線方式
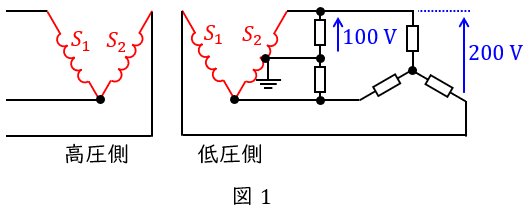
図1に示すように，低圧側の電灯\( \ 100 \ \mathrm {[V]} \ \)負荷と動力\( \ 200 \ \mathrm {[V]} \ \)負荷の両方に電力を供給することが可能な配電方式です。
三相負荷のみに供給する変圧器\( \ \mathrm {S}_{1} \ \)を専用変圧器，単相負荷と三相負荷の両方に供給する変圧器\( \ \mathrm {S}_{2} \ \)を共用変圧器，といいます。
単相負荷の分だけ共用変圧器の方が容量が多く必要とする\( \ \left( \mathrm {S}_{2}＞\mathrm {S}_{1}\right) \ \)ので，異容量\( \ \mathrm {V} \ \)結線といいます。

【解答】

(a)解答：(2)
三相平衡負荷の力率は進み\( \ \displaystyle \frac {\pi }{6} \ \mathrm {[rad]} \ \)なので，各相の電圧と電流の関係は図2のようになる。

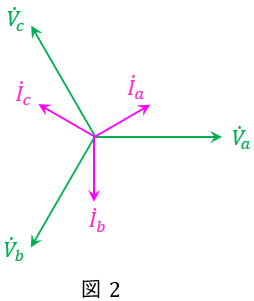
次に，\( \ {\dot V}_{ab} \ \)は\( \ \mathrm {a} \ \)相と\( \ \mathrm {b} \ \)相の間の電圧なので，ベクトル図上では図3のようになる。

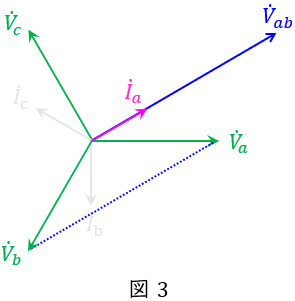
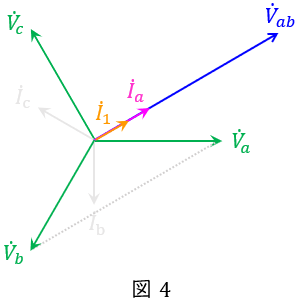
また，単相負荷\( \ \mathrm {P} \ \)の力率は\( \ 1 \ \)なので，\( \ {\dot V}_{ab} \ \)と\( \ {\dot I}_{1} \ \)は同相となり，図4のようになる。
以上から，解答は(2)と求められる。

(b)解答：(3)
単相負荷の電力を\( \ P_{1} \ \mathrm {[kW]} \ \)，三相負荷の電力を\( \ P_{3}=45 \ \mathrm {[kW]} \ \)とおく。それぞれの負荷電流\( \ I_{1} \ \mathrm {[A]} \ \)及び\( \ I_{a} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {P_{1}\times 10^{3}}{V_{ab}} \\[ 5pt ] I_{3}&=&\frac {P_{3}}{\displaystyle \sqrt {3}V_{ab}\cos \frac {\pi }{6} } \\[ 5pt ] &=&\frac {45\times 10^{3}}{\displaystyle \sqrt {3}V_{ab}\frac {\sqrt {3}}{2} } \\[ 5pt ] &=&\frac {30\times 10^{3}}{V_{ab}} \\[ 5pt ] \end{eqnarray}
\] となり，(a)より，\( \ {\dot I}_{a} \ \)と\( \ {\dot I}_{1} \ \)は同相であるから，変圧器\( \ \mathrm {T_{1}} \ \)を流れる電流\( \ I_{ab} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{ab}&=&I_{1}+I_{3} \\[ 5pt ] &=&\frac {P_{1}\times 10^{3}}{V_{ab}}+\frac {30\times 10^{3}}{V_{ab}} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ \mathrm {T_{1}}=V_{ab}I_{ab}=75 \ \mathrm {[kV\cdot A]} \ \)であるから，
\[
\begin{eqnarray}
V_{ab}I_{ab}&=&V_{ab}\left( \frac {P_{1}\times 10^{3}}{V_{ab}}+\frac {30\times 10^{3}}{V_{ab}}\right) \\[ 5pt ] 75\times 10^{3}&=&P_{1}\times 10^{3}+30\times 10^{3} \\[ 5pt ] P_{1}&=&45 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。