Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
負荷設備(低圧のみ)の容量が\( \ 600 \ \mathrm {[kW]} \ \),需要率が\( \ 60 \ \mathrm {[%]} \ \)の高圧需要家について,次の(a)及び(b)に答えよ。
(a) 下表に示す受電用変圧器バンク容量\( \ \mathrm {[kV\cdot A]} \ \)が選択できる。
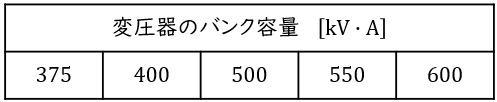
この中から,この需要家に設置すべき必要最小限の変圧器バンク容量\( \ \mathrm {[kV\cdot A]} \ \)として選ぶとき,正しいのは次のうちどれか。
ただし,負荷設備の総合力率は\( \ 0.8 \ \)とする。
(1) \( \ 375 \ \) (2) \( \ 400 \ \) (3) \( \ 500 \ \) (4) \( \ 550 \ \) (5) \( \ 600 \ \)
(b) 年負荷率を\( \ 55 \ \mathrm {[%]} \ \)とするとき,負荷の年間総消費電力量\( \ \mathrm {[MW\cdot h]} \ \)の値として,最も近いのは次のうちどれか。
ただし,\( \ 1 \ \)年間の日数は\( \ 365 \ \)日とする。
(1) \( \ 1 \ 665 \ \) (2) \( \ 1 \ 684 \ \) (3) \( \ 1 \ 712 \ \) (4) \( \ 1 \ 734 \ \) (5) \( \ 1 \ 754 \ \)
【ワンポイント解説】
需要家に設置すべき変圧器のバンク容量と需要家の年間消費電力量を求める問題です。
電力科目や機械科目で学習した内容と法規科目の需要率,不等率を組み合わせた総合問題となっています。
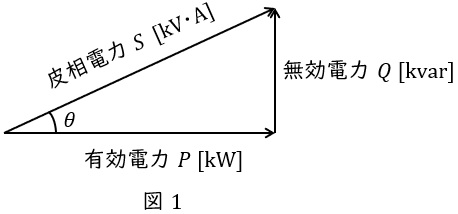
1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図1のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図1において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.需要率,不等率,負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
②不等率(常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ]
\end{eqnarray}
\]
③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(3)
負荷設備の容量が\( \ 600 \ \mathrm {[kW]} \ \),需要率が\( \ 60 \ \mathrm {[%]} \ \)なので,負荷の最大電力\( \ P_{m} \ \mathrm {[kW]} \ \)は,ワンポイント解説「2.需要率,不等率,負荷率の定義」の通り,
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100 \\[ 5pt ]
60&=&\frac {P_{m}}{600}\times 100 \\[ 5pt ]
P_{m}&=&\frac {60\times 600}{100} \\[ 5pt ]
&=&360 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となり,力率\( \ \cos \theta =0.8 \ \)であるから,負荷の最大皮相電力\( \ S_{m} \ \mathrm {[kV\cdot A]} \ \)は,ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り,
\[
\begin{eqnarray}
S_{m}&=&\frac {P_{m}}{\cos \theta } \\[ 5pt ]
&=&\frac {360}{0.8} \\[ 5pt ]
&=&450 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,表の中で選択すべき変圧器バンク容量は\( \ 500 \ \mathrm {[kV\cdot A]} \ \)と求められる。
(b)解答:(4)
年負荷率が\( \ 55 \ \mathrm {[%]} \ \)なので,負荷の平均電力\( \ P_{a} \ \mathrm {[kW]} \ \)は,ワンポイント解説「2.需要率,不等率,負荷率の定義」の通り,
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100 [%] \\[ 5pt ]
55&=&\frac { P_{a}}{ P_{m}}\times 100 \\[ 5pt ]
P_{a}&=&\frac {55P_{m}}{100} \\[ 5pt ]
&=&\frac {55\times 360}{100} \\[ 5pt ]
&=&198 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,負荷の年間総消費電力量\( \ W \ \mathrm {[MW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W&=&P_{a}\times 24\times 365 \\[ 5pt ]
&=&198\times 24\times 365 \\[ 5pt ]
&≒&1 \ 734 \ 000 \ \mathrm {[kW\cdot h]} → 1 \ 734 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは