《理論》〈電気回路〉[R07上:問9]交流回路の負荷接続による電流変化からの抵抗値の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図の交流回路において，電源電圧を\( \ E= 140 \ \mathrm {V} \ \)とする。この電源に抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)と誘導性リアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)とからなる力率\( \ 0.8 \ \)の誘導性負荷を接続したところ，電源から流れ出る電流の大きさは\( \ 30 \ \mathrm {A} \ \)であった。次に，スイッチ\( \ \mathrm {S} \ \)を閉じ，誘導性負荷と並列に抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を接続すると，電源から流れ出る電流の大きさが\( \ 82 \ \mathrm {A} \ \)となった。このとき，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.5 \ \)　　(2)　\( \ 2.3 \ \)　　(3)　\( \ 2.5 \ \)　　(4)　\( \ 2.9 \ \)　　(5)　\( \ 3.0 \ \)

【ワンポイント解説】

交流回路のスイッチを閉じた前後における電流値の変化から抵抗値を導出する問題です。
交流回路の場合は位相が関係しているため，電圧と電流のベクトル図をしっかりと描けることが重要です。また，交流回路で定番となる三平方の定理の計算についても解答を参照しながら，できるだけ電卓に頼らないように工夫するようにしましょう。
本問は平成23年問8の数値を変えた類題となります。

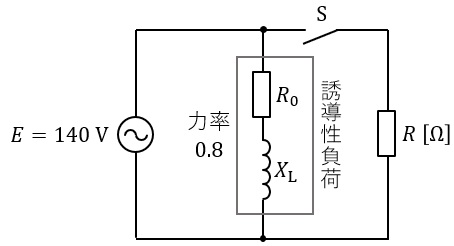
1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(3)
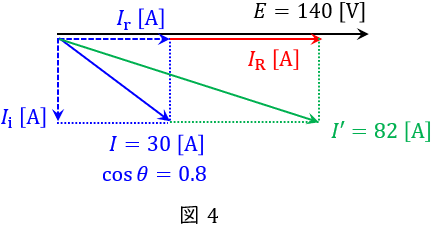
題意に沿ってベクトル図を描くと図4のようになる。
図4において，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)接続前の電流\( \ I=30 \ \mathrm {[A]} \ \)について，電源電圧\( \ E \ \mathrm {[V]} \ \)と同相成分\( \ I_{\mathrm {r}} \ \mathrm {[A]} \ \)，電源電圧\( \ E \ \mathrm {[V]} \ \)から\( \ 90^{\circ } \ \)遅れた電流成分\( \ I_{\mathrm {i}} \ \mathrm {[A]} \ \)は，誘導性負荷の力率\( \ \cos \theta =0.8 \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {r}}&=&I\cos \theta \\[ 5pt ] &=&30\times 0.8 \\[ 5pt ] &=&24 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {i}}&=&I\sin \theta \\[ 5pt ] &=&I\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&30\times \sqrt {1-0.8^{2}} \\[ 5pt ] &=&30\times 0.6 \\[ 5pt ] &=&18 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)接続後，\( \ R \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}}&=&\frac {E}{R} \\[ 5pt ] &=&\frac {140}{R} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ R \ \mathrm {[\Omega ]} \ \)を接続した後の，電源から流れ出る電流の大きさ\( \ I^{\prime }=82 \ \mathrm {[A]} \ \)であることから，図4に三平方の定理を適用し各値を代入すると，
\[
\begin{eqnarray}
{I^{\prime }}^{2}&=&\left( I_{\mathrm {r}}+I_{\mathrm {R}} \right) ^{2}+I_{\mathrm {i}}^{2} \\[ 5pt ] 82^{2}&=&\left( 24+\frac {140}{R} \right) ^{2}+18^{2} \\[ 5pt ] 6 \ 724&=&\left( 24+\frac {140}{R} \right) ^{2}+324 \\[ 5pt ] \left( 24+\frac {140}{R} \right) ^{2}&=&6 \ 400 \\[ 5pt ] 24+\frac {140}{R} &=&80 \\[ 5pt ] \frac {140}{R} &=&56 \\[ 5pt ] R &=&\frac {140}{56} \\[ 5pt ] &=&2.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。