【問題】
【難易度】★★☆☆☆(やや易しい)
交流回路に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし,抵抗\(R \ \mathrm {[\Omega ]}\),インダクタンス\(L \ \mathrm {[H ]}\),静電容量\(C \ \mathrm {[F ]}\)とする。
(1) 正弦波交流起電力の最大値を\(E_{\mathrm {m}} \ \mathrm {[V]}\),平均値を\(E_{\mathrm {a}} \ \mathrm {[V]}\)とすると,平均値と最大値の関係は,理論的に次のように表される。
\[
E_{\mathrm {a}}=\frac {2E_{\mathrm {m}}}{\pi }≒0.637E_{\mathrm {m}} \ \mathrm {[V]}
\]
(2) ある交流起電力の時刻\(t \ \mathrm {[s]}\)における瞬時値が,\(e=100\sin 100\pi t \ \mathrm {[V]}\)であるとすると,この起電力の周期は\(20 \ \mathrm {ms}\)である。
(3) \(RLC\)直列回路に角周波数\(\omega \ \mathrm {[rad/s]}\)の交流電圧を加えたとき,\(\displaystyle \omega L > \frac {1}{\omega C}\)の場合,回路を流れる電流の位相は回路に加えた電圧より遅れ,\(\displaystyle \omega L < \frac {1}{\omega C}\)の場合,回路を流れる電流の位相は回路に加えた電圧より進む。
(4) \(RLC\)直列回路に角周波数\(\omega \ \mathrm {[rad/s]}\)の交流電圧を加えたとき,\(\displaystyle \omega L = \frac {1}{\omega C}\)の場合,回路のインピーダンス\(Z \ \mathrm {[\Omega ]}\)は,\(Z=R \ \mathrm {[\Omega ]}\)となり,回路に加えた電圧と電流は同相になる。この状態を回路の共振状態であるという。
(5) \(RLC\)直列回路のインピーダンス\(Z \ \mathrm {[\Omega ]}\),電力\(P \ \mathrm {[W]}\)及び皮相電力\(S \ \mathrm {[V\cdot A ]}\)を使って回路の力率\(\cos \theta \)を表すと,\(\cos \theta =\displaystyle \frac {R}{Z}\),\(\cos \theta =\displaystyle \frac {S}{P}\)の関係がある。
【ワンポイント解説】
誤答選択問題ですが,中身は計算問題のような内容です。誤答が見つけやすい問題なので,できれば本番では間違えたくないレベルと言えると思います。
【関連する「電気の神髄」記事】
【解答】
解答:(5)
(1):正しい
この選択肢を正確に解くためには積分の知識が必要です。わからない場合は保留にしておくと良いと思います。
正弦波交流の平均値を求めると,
\[
\begin{eqnarray}
E_{\mathrm {a}} &=&\frac {1}{\pi } \int _{0}^{\pi } E_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ]
&=&\frac {2E_{\mathrm {m}}}{\pi } \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(2):正しい
\(e=100\sin 100\pi t \ \mathrm {[V]}\)において,\(\displaystyle \omega =\frac {2\pi }{T}=100\pi \)であるから,
\[
\begin{eqnarray}
\frac {2\pi }{T} &=& 100\pi \\[ 5pt ]
T &=&0.02 \ \mathrm {[s]} → 20 \ \mathrm {[ms]} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(3):正しい
問題点の通り,リアクトル\(L\)は電流の位相を遅らせ,\(C\)は電流の位相を進ませます。従って,その大小により遅れと進みが決まります。
(4):正しい
問題文の通りです。
(5):誤り
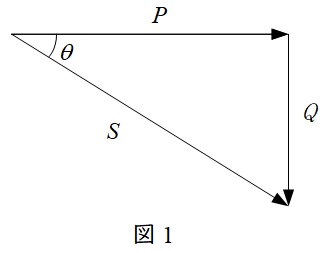
皮相電力を\(S \ \mathrm {[V\cdot A ]}\),有効電力を\(P \ \mathrm {[W]}\),無効電力を\(Q \ \mathrm {[var ]}\)とすると,図1のような関係があり,力率\(\cos \theta \)は\(\displaystyle \frac {P}{S}\)となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは