Contents
【問題】
【難易度】★★★☆☆(普通)
無線通信で行われるアナログ変調・復調に関する記述について,次の(a)及び(b)の問に答えよ。
(a) 無線通信で音声や画像などの情報を送る場合,送信側においては,情報を電気信号(信号波)に変換する。次に信号波より\( \ \fbox { (ア) } \ \)周波数の搬送波に信号波を含ませて得られる信号を送信する。受信側では,搬送波と信号波の二つの成分を含むこの信号から\( \ \fbox { (イ) } \ \)の成分だけを取り出すことによって,音声や画像などの情報を得る。
搬送波に信号波を含ませる操作を変調という。\( \ \fbox { (ウ) } \ \)の搬送波を用いる基本的な変調方式として,振幅変調\( \ \left( \mathrm {AM}\right) \ \),周波数変調\( \ \left( \mathrm {FM}\right) \ \),位相変調\( \ \left( \mathrm {PM}\right) \ \)がある。
搬送波を変調して得られる信号からもとの信号波を取り出す操作を復調又は\( \ \fbox { (エ) } \ \)という。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 高い & 信号波 & 三角波 & 検波 \\
\hline
(2) & 高い & 信号波 & 正弦波 & 検波 \\
\hline
(3) & 高い & 搬送波 & 三角波 & 増幅 \\
\hline
(4) & 低い & 信号波 & 三角波 & 増幅 \\
\hline
(5) & 低い & 搬送波 & 正弦波 & 検波 \\
\hline
\end{array}
\]
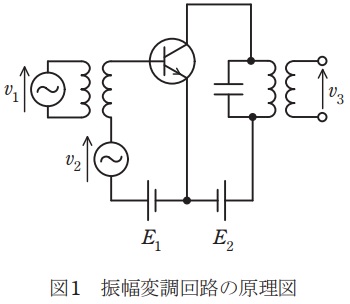
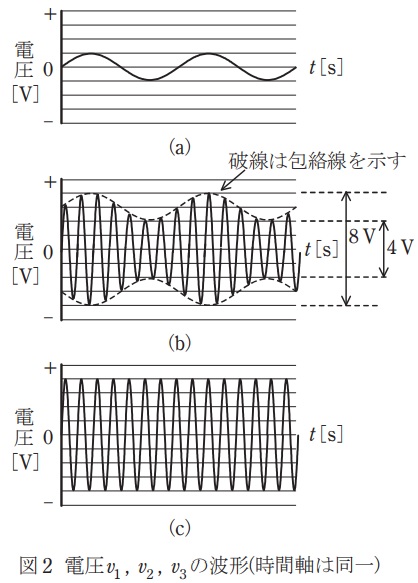
(b) 図1は,トランジスタの\( \ \fbox { (ア) } \ \)に信号波の電圧を加えて振幅変調を行う回路の原理図である。電圧\( \ v_{1} \ \),\( \ v_{2} \ \),\( \ v_{3} \ \)の波形を同時に計測したところ図2のいずれかであった。このとき,電圧\( \ v_{1} \ \)の波形は\( \ \fbox { (イ) } \ \),\( \ v_{2} \ \)の波形は\( \ \fbox { (ウ) } \ \),\( \ v_{3} \ \)の波形は\( \ \fbox { (エ) } \ \)である。図2のグラフより振幅変調の変調率を計算すると約\( \ \fbox { (オ) } \ \mathrm {%} \ \)となる。
上記の記述中の空白箇所(ア)~(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,図2のそれぞれの電圧波形間の位相関係は無視するものとする。
\[
\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & コレクタ & 図 \ 2 \left( \mathrm {c}\right) & 図 \ 2 \left( \mathrm {a}\right) & 図 \ 2 \left( \mathrm {b}\right) & 33 \\
\hline
(2) & コレクタ & 図 \ 2 \left( \mathrm {c}\right) & 図 \ 2 \left( \mathrm {b}\right) & 図 \ 2 \left( \mathrm {a}\right) & 67 \\
\hline
(3) & ベース & 図 \ 2 \left( \mathrm {b}\right) & 図 \ 2 \left( \mathrm {a}\right) & 図 \ 2 \left( \mathrm {c}\right) & 50 \\
\hline
(4) & エミッタ & 図 \ 2 \left( \mathrm {b}\right) & 図 \ 2 \left( \mathrm {c}\right) & 図 \ 2 \left( \mathrm {a}\right) & 67 \\
\hline
(5) & ベース & 図 \ 2 \left( \mathrm {c}\right) & 図 \ 2 \left( \mathrm {a}\right) & 図 \ 2 \left( \mathrm {b}\right) & 33 \\
\hline
\end{array}
\]
【ワンポイント解説】
無線通信で行われるアナログ変調・復調に関する問題です。
基本的に選択問題で出題される内容ですが,計算量が少ない問題が多いため,勉強しておくと得点源となり得る問題です。
本問は平成20年問18からの再出題となります。
1.無線通信における信号の伝送
図3に示すように,無線通信においては,信号波と呼ばれる送りたい情報及び周波数のより高い搬送波と呼ばれる信号を送信機によって合成し,変調波を作って送信します。
搬送波の振幅に対する信号波の振幅の大きさ\( \ \displaystyle \frac {a_{1}}{a_{2}} \ \)を変調波の変調度といいます。
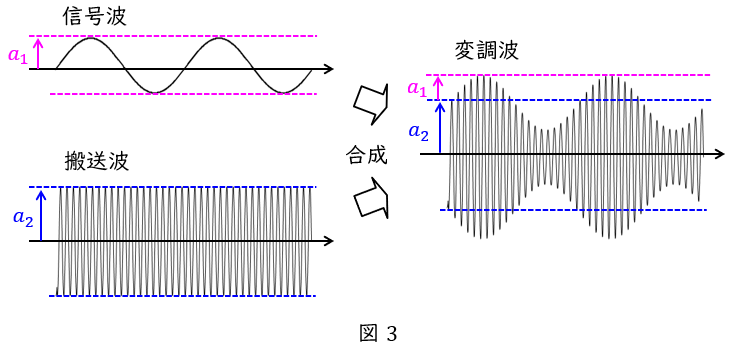
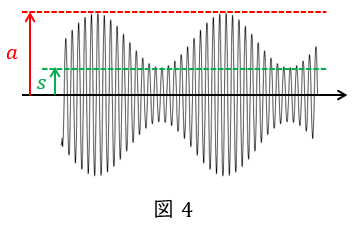
もし,変調波のみが与えられている場合には変調波の振幅の最大値\( \ a \ \)及び最小値\( \ s \ \)であるとき,\( \ \displaystyle \frac {a-s}{a+s} \ \)でも求めることができます。
2.信号の変調
信号の変調には振幅の変化で変調する振幅変調\( \ \left( \mathrm {AM}\right) \ \),周波数の変化で変調する周波数変調\( \ \left( \mathrm {FM}\right) \ \),位相の変化で変調する位相変調\( \ \left( \mathrm {PM}\right) \ \)があり,以下の通りとなります。アナログで説明していますが,ディジタルでもほぼ同じです。
①振幅変調\( \ \left( \mathrm {AM}\right) \ \)
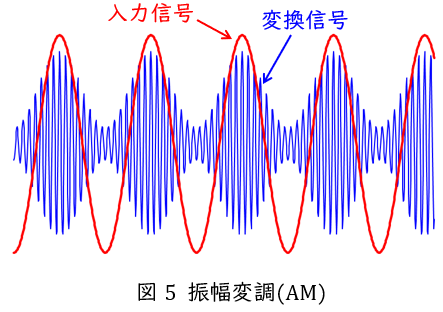
図5のように入力信号を搬送波と呼ばれる高調波の正弦波によって振幅に変化させ伝送路に適した波形に変換する方法です。図5において赤線が入力,青線が出力となります。振幅変調は波形のひずみの影響を受けやすい特徴があります。
②周波数変調\( \ \left( \mathrm {FM}\right) \ \)
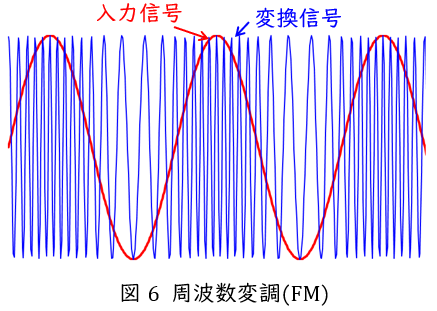
図6のように入力信号を搬送波と呼ばれる高調波の正弦波によって周波数に変化させ伝送路に適した波形に変換する方法です。図6において赤線が入力,青線が出力となります。周波数変調は振幅変調よりも広い周波数帯域を使用します。
③位相変調\( \ \left( \mathrm {PM}\right) \ \)
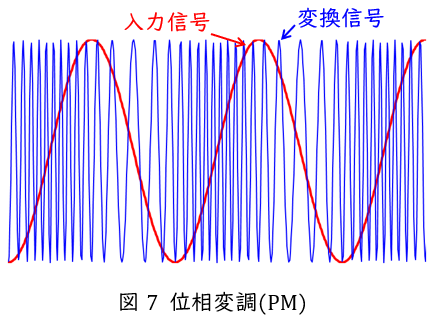
図7のように入力信号を搬送波と呼ばれる高調波の正弦波によって位相に変化させ伝送路に適した波形に変換する方法です。周波数変調と似たような形となりますが,位相変調では入力信号を時間微分したものを周波数変調させたような形となります。図7において赤線が入力,青線が出力となります。
【解答】
(a)解答:(2)
(ア)
ワンポイント解説「1.無線通信における信号の伝送」の通り,搬送波は信号波より高い周波数となります。
(イ)
受信側では,搬送波を取り除き信号波の成分だけ取り出すことによって,音声や画像などの情報を得ることになります。
(ウ)
ワンポイント解説「2.信号の変調」の通り,正弦波の搬送波を用いる基本的な変調方式として,振幅変調\( \ \left( \mathrm {AM}\right) \ \),周波数変調\( \ \left( \mathrm {FM}\right) \ \),位相変調\( \ \left( \mathrm {PM}\right) \ \)があります。
(エ)
搬送波を変調して得られる信号からもとの信号波を取り出す操作を復調又は検波といいます。
(b)解答:(5)
(ア)
図1は,入力がベース,出力がコレクタの回路となります。
(イ)
題意より\( \ v_{1} \ \)は搬送波なので,ワンポイント解説「2.信号の変調」の通り,図\( \ 2 \left( \mathrm {c}\right) \ \)となります。
(ウ)
\( \ v_{2} \ \)は信号波なので,ワンポイント解説「2.信号の変調」の通り,図\( \ 2 \left( \mathrm {a}\right) \ \)となります。
(エ)
\( \ v_{3} \ \)はトランジスタの出力で変調波なので,ワンポイント解説「2.信号の変調」の通り,図\( \ 2 \left( \mathrm {b}\right) \ \)となります。
(オ)
ワンポイント解説「1.無線通信における信号の伝送」の通り,変調率は,
\[
\begin{eqnarray}
\displaystyle \frac {4-2}{4+2} &≒&0.33 → 33 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは