《機械》〈照明〉[H26:問17]球形光源の基本公式に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

均等放射の球形光源（球の直径は\( \ 30 \ \mathrm {cm} \ \)）がある。床からこの球形光源の中心までの高さは\( \ 3 \ \mathrm {m} \ \)である。また，球形光源から放射される全光束は\( \ 12 \ 000 \ \mathrm {lm} \ \)である。次の(a)及び(b)の問に答えよ。

(a)　球形光源直下の床の水平面照度の値\( \ \mathrm {[lx]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，天井や壁など，周囲からの反射光の影響はないものとする。

　(1)　\( \ 35 \ \)　　(2)　\( \ 106 \ \)　　(3)　\( \ 142 \ \)　　(4)　\( \ 212 \ \)　　(5)　\( \ 425 \ \)

(b)　球形光源の光度の値\( \ \mathrm {[cd]} \ \)と輝度の値\( \ \mathrm {[cd/m^{2}]} \ \)との組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 　光度　 & 　輝度　 \\
\hline
(1) & 　1 \ 910　 & 　1 \ 010　 \\
\hline
(2) & 　955　 & 　3 \ 380　 \\
\hline
(3) & 　955　 & 　13 \ 500　 \\
\hline
(4) & 　1 \ 910　 & 　27 \ 000　 \\
\hline
(5) & 　3 \ 820　 & 　13 \ 500　 \\
\hline
\end{array}
\]

【ワンポイント解説】

照明の問題は慣れてしまうと比較的易しい問題が多いのが特徴です。本問は過去問等の習熟を通して確実に得点できるようにしましょう。

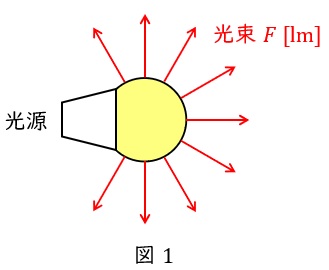
1.光束\( \ F \ \)
光源から出る可視光の量（エネルギー）で，単位は\( \ \mathrm {[lm]} \ \)となります。
電磁気の分野の電束に似たようなイメージで良いです。

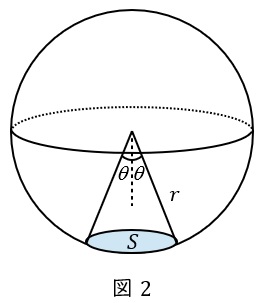
2.立体角の定義
図2のように球体があり，半径\( \ r \ \mathrm {[m]} \ \)の錐体が球面を切り取った時の面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると，立体角\( \ \omega \ \mathrm {[sr]} \ \)は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角\( \ \theta \ \mathrm {[rad]} \ \)で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は\( \ \theta = \pi \ \)の時であり，\( \ \omega =4\pi \ \)となります。

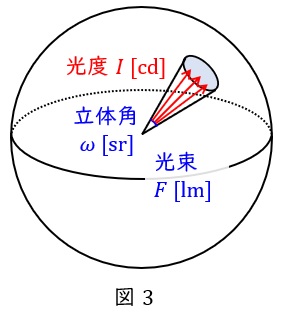
3.光度\( \ I \ \)
ある方向に向かう光束\( \ F \ \mathrm {[lm]} \ \)を立体角\( \ \omega \ \mathrm {[sr]} \ \)で割ったもので，光度\( \ I \ \mathrm {[cd]} \ \)を式で表すと，
\[
\begin{eqnarray}
I &=&\frac {F}{\omega } \\[ 5pt ] \end{eqnarray}
\] となります。

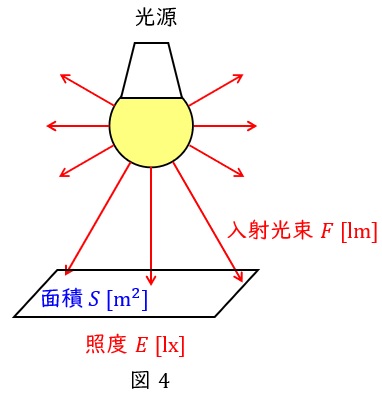
4.照度\( \ E \ \)
図4のように，面積\( \ S \ \mathrm {[m^{2}]} \ \)へ入射する光束が\( \ F \ \mathrm {[lm]} \ \)であるとき，平均照度\( \ E \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ] \end{eqnarray}
\] となり，光源からある方向へ向かう光度が\( \ I \ \mathrm {[cd]} \ \)であるとき，光源からの距離\( \ l \ \mathrm {[m]} \ \)離れた垂直面の照度\( \ E \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ] &=&\frac {4\pi I}{4\pi l^{2}} \\[ 5pt ] &=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このように，一般に物理量が\( \ 2 \ \)乗に反比例する法則を逆\( \ 2 \ \)乗の法則といいます。

5.輝度\( \ L \ \)
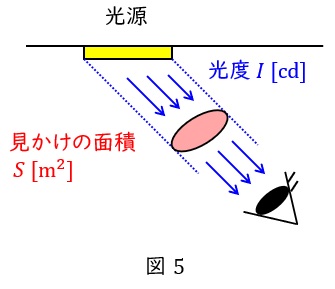
図5のように，ある方向から見た光源のまぶしさを表す指標で，光源からある方向へ向かう光度が\( \ I \ \mathrm {[cd]} \ \)であるとき，輝度\( \ L \ \mathrm {[cd/m^{2}]} \ \)は，同じ方向から照明を見た投影面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると，
\[
\begin{eqnarray}
L&=&\frac {I}{S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(2)
均等放射の球形光源から床に向かう光度\( \ I \ \mathrm {[cd]} \ \)は，球形光源の全光束が\( \ F=12 \ 000 \ \mathrm {[lm]} \ \)であるから，ワンポイント解説「2.立体角の定義」及び「3.光度\( \ I \ \)」の通り，
\[
\begin{eqnarray}
I &=&\frac {F}{4\pi } \\[ 5pt ] &=&\frac {12 \ 000}{4\pi } \\[ 5pt ] &≒&954.9 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，球形光源の直下における水平面照度\( \ E \ \mathrm {[lx]} \ \)の大きさは，光源からの距離\( \ l=3 \ \mathrm {[m]} \ \)なので，ワンポイント解説「4.照度\( \ E \ \)」の通り，
\[
\begin{eqnarray}
E &=&\frac {I}{l^{2}} \\[ 5pt ] &=&\frac {954.9}{3^{2}} \\[ 5pt ] &=&106.1　→　106 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
(a)より，球形光源の光度\( \ I=954.9 \ → \ 955 \ \mathrm {[cd]} \ \)と求められる。

また，球形光源をみたときの投影面積\( \ S \ \mathrm {[m^{2}]} \ \)は，球形光源の直径が\( \ D=0.3 \ \mathrm {[m]} \ \)より，
\[
\begin{eqnarray}
S &=&\pi \left( \frac {D}{2}\right) ^{2} \\[ 5pt ] &=&\pi \times \left( \frac {0.3}{2}\right) ^{2} \\[ 5pt ] &≒&0.0706 \ 9 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] となるので，光源の輝度\( \ L \ \mathrm {[cd/m^{2}]} \ \)は，ワンポイント解説「5.輝度\( \ L \ \)」の通り，
\[
\begin{eqnarray}
L &=&\frac {I}{S} \\[ 5pt ] &=&\frac {954.9}{0.0706 \ 9} \\[ 5pt ] &≒&13 \ 508　→　13 \ 500 \ \mathrm {[cd/m^{2}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。