Contents
【問題】
【難易度】★★★☆☆(普通)
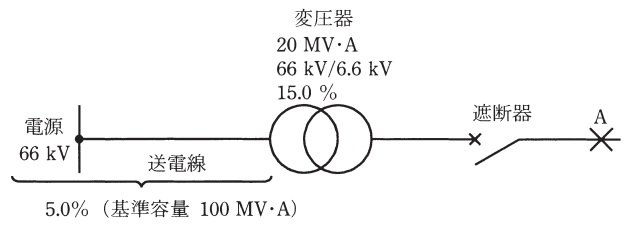
図に示すように,定格電圧\( \ 66 \ \mathrm {[kV]} \ \)の電源から送電線と三相変圧器を介して,二次側に遮断器が接続された系統を考える。三相変圧器の電気的特性は,定格容量\( \ 20 \ \mathrm {[MV\cdot A]} \ \),一次側線間電圧\( \ 66 \ \mathrm {[kV]} \ \),二次側線間電圧\( \ 6.6 \ \mathrm {[kV]} \ \),自己容量基準での百分率リアクタンス\( \ 15.0 \ \mathrm {[%]} \ \)である。一方,送電線から電源側をみた電気的特性は,基準容量\( \ 100 \ \mathrm {[MV\cdot A]} \ \)の百分率インピーダンスが\( \ 5.0 \ \mathrm {[%]} \ \)である。このとき,次の(a)及び(b)の問に答えよ。
ただし,百分率インピーダンスの抵抗分は無視するものとする。
(a) 基準容量を\( \ 10 \ \mathrm {[MV\cdot A]} \ \)としたとき,変圧器の二次側から電源側をみた百分率リアクタンス\( \ \mathrm {[%]} \ \)の値として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 2.0 \ \) (2) \( \ 8.0 \ \) (3) \( \ 12.5 \ \) (4) \( \ 15.5 \ \) (5) \( \ 20.0 \ \)
(b) 図の\( \ \mathrm {A} \ \)で三相短絡事故が発生したとき,事故電流\( \ \mathrm {[kA]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,変圧器の二次側から\( \ \mathrm {A} \ \)までのインピーダンス及び負荷は,無視するものとする。
(1) \( \ 4.4 \ \) (2) \( \ 6.0 \ \) (3) \( \ 7.0 \ \) (4) \( \ 11 \ \) (5) \( \ 44 \ \)
【ワンポイント解説】
(a)は比較的易しい問題,(b)も三相短絡電流と百分率インピーダンスとの関係を知っていれば難なく解けると思います。百分率インピーダンスは苦手意識を持っている受験生も多いので,きちんと勉強していれば差をつけることができる問題と言えると思います。
1.百分率インピーダンス容量換算
基準容量を\( \ P_{\mathrm {n}} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \),基準電流を\( \ I_{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となるため,百分率インピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の百分率インピーダンスは,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}%Z_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ %Z \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z/100} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※百分率インピーダンスの定義式等から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
【解答】
(a)解答:(2)
送電線の百分率インピーダンスと変圧器の百分率リアクタンスを\( \ 10 \ \mathrm {[MV\cdot A]} \ \)換算すると,
\[
\begin{eqnarray}
\frac {10}{100}\times 5 &=&0.5 \ \mathrm {[%]} \\[ 5pt ]
\frac {10}{20}\times 15 &=&7.5 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,変圧器の二次側から見た百分率リアクタンスの大きさは,
\[
\begin{eqnarray}
0.5+7.5 &=&8.0 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
基準電流\( \ I_{\mathrm {n}} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {n}} &=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ]
&≒&874.8 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,ワンポイント解説「2.百分率インピーダンスの短絡電流計算」より,短絡電流\( \ I_{\mathrm {s}} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
&=&\frac {100\times 874.8}{8} \\[ 5pt ]
&≒&11000 \ \mathrm {[A]} → 11 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは