《電力》〈送電〉[R2:問16]三相平衡負荷を流れる電流及び送電損失に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

こう長\( \ 25 \ \mathrm {km} \ \)の三相\( \ 3 \ \)線式\( \ 2 \ \)回線送電線路に，受電端電圧が\( \ 22 \ \mathrm {kV} \ \)，遅れ力率\( \ 0.9 \ \)の三相平衡負荷\( \ 5 \ 000 \ \mathrm {kW} \ \)が接続されている。次の(a)及び(b)の問に答えよ。ただし，送電線は\( \ 2 \ \)回線運用しており，与えられた条件以外は無視するものとする。

(a)　送電線\( \ 1 \ \)線あたりの電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，送電線は単導体方式とする。

　(1)　\( \ 42.1 \ \)　　(2)　\( \ 65.6 \ \)　　(3)　\( \ 72.9 \ \)　　(4)　\( \ 126.3 \ \)　　(5)　\( \ 145.8 \ \)

(b)　送電損失を三相平衡負荷に対し\( \ 5 \ \mathrm {％} \ \)以下にするための送電線\( \ 1 \ \)線の最小断面積の値\( \ \mathrm {[{mm}^{2}]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，使用電線は，断面積\( \ 1 \ \mathrm {{mm}^{2}} \ \)，長さ\( \ 1 \ \mathrm {m} \ \)当たりの抵抗を\( \ \displaystyle \frac {1}{35} \ \mathrm {\Omega } \ \)とする。

　(1)　\( \ 31 \ \)　　(2)　\( \ 46 \ \)　　(3)　\( \ 74 \ \)　　(4)　\( \ 92 \ \)　　(5)　\( \ 183 \ \)

【ワンポイント解説】

送電損失に関する計算問題は，電力科目の中では定番の問題です。電圧降下の問題と合わせて，確実に理解しておくと，合格がグッと近づくと思います。
本問の三相\( \ 3 \ \)線式や\( \ 2 \ \)回線といったところが引っ掛けとなっているところに注意し，\( \ \sqrt {3} \ \)や\( \ 2 \ \)で割ることを忘れないようにしましょう。
平成24年問10の問題と非常に似ているので，過去問をしっかり勉強されていた方なら難なく解けると良いと思います。

1.三相\( \ 3 \ \)線式線路の有効電力\( \ P \ \)
三相\( \ 3 \ \)線式の送電線の線間電圧が\( \ V \ \)，線電流が\( \ I \ \)，電圧と電流の力率が\( \ \cos \theta \ \)であるとき，送電電力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] となります。

2.抵抗率\( \ \rho \ \)
送電線の断面積\( \ 1 \ \mathrm {[{m}^{2}]} \ \)及び長さ\( \ 1 \ \mathrm {[m]} \ \)当たりの抵抗値\( \ \rho \ \mathrm {[\Omega \cdot m]} \)が与えられている時，断面積\( \ S \ \mathrm {[{m}^{2}]} \ \)，長さ\( \ l \ \mathrm {[m]} \ \)の送電線の抵抗\( \ R \ \mathrm {[\Omega]} \)の大きさは，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
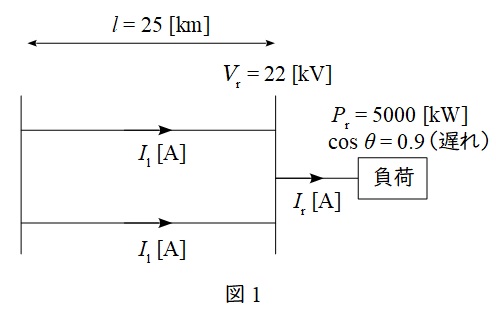
題意に沿って，単線図を描くと図1のようになる。
図1より，受電端から負荷に流れる電流\( \ I_{\mathrm {r}} \ \mathrm {[A]} \ \)の大きさは，ワンポイント解説「1.三相\( \ 3 \ \)線式の有効電力\( \ P \ \)」より，
\[
\begin{eqnarray}
I_{\mathrm {r}} &=&\frac {P_{\mathrm {r}}}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] &=&\frac {5000\times 10^{3}}{\sqrt {3}\times 22\times 10^{3} \times 0.9 } \\[ 5pt ] &≒&145.80 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，送電線\( \ 1 \ \)線あたりの電流\( \ I_{\mathrm {l}} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {l}} &=&\frac {I_{\mathrm {r}}}{2} \\[ 5pt ] &=&\frac {145.80}{2} \\[ 5pt ] &≒&72.90　→　72.9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
送電線\( \ 1 \ \)線当たりの抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)は，断面積を\( \ S \ \mathrm {[{mm}^{2}]} \ \)とすると，ワンポイント解説「2.抵抗率\( \ \rho \ \)」より，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{35} \times 25\times 10^{3}}{S} \\[ 5pt ] &≒&\frac {714.3}{S} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，送電線の損失\( \ P_{\mathrm {l}} \ \mathrm {[kW]} \ \)は，三相\( \ 3 \ \)線式\( \ 2 \ \)回線であることに注意すると，
\[
\begin{eqnarray}
P_{\mathrm {l}} &=&2\times 3RI_{\mathrm {l}}^{2} \\[ 5pt ] &=&6\times \frac {714.3}{S} \times 72.90^{2} \\[ 5pt ] &≒&\frac {22780000}{S} \ \mathrm {[W]}　→　\frac {22780}{S} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，この値が受電電力の\( \ 5 \ \mathrm {[％]} \ \)以下にならなければならないので，
\[
\begin{eqnarray}
P_{\mathrm {l}} &=&0.05 P_{\mathrm {r}} \\[ 5pt ] \frac {22780}{S}&=&0.05 \times 5000 \\[ 5pt ] \frac {22780}{S}&=&250 \\[ 5pt ] S&≒&91.1 \ \mathrm {[{mm}^{2}]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ 5 \ \mathrm {[％]} \ \)以下にするために繰り上げすると，\( \ 92 \ \mathrm {{mm}^{2}} \ \)と求められる。