《電力》〈送電〉[R01:問16]送電線のフェランチ現象に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

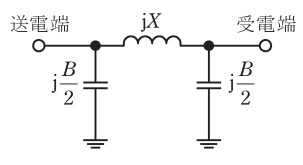
送電線のフェランチ効果に関する問である。三相\( \ 3 \ \)線式\( \ 1 \ \)回線送電線の一相が図の\( \ \pi \ \)形等価回路で表され，送電線路のインピーダンス\( \ \mathrm {j}X=\mathrm {j}200 \ \mathrm {[\Omega ]} \ \)，アドミタンス\( \ \mathrm {j}B=\mathrm {j}0.800 \ \mathrm {[mS]} \ \)とし，送電端の線間電圧が\( \ 66.0 \ \mathrm {[kV ]} \ \)であり，受電端が無負荷のとき，次の(a)及び(b)の問に答えよ。

(a)　受電端の線間電圧の値\( \ \mathrm {[kV]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(66.0\)　　(2)　\(71.7\)　　(3)　\(78.6\)　　(4)　\(114\)　　(5)　\(132\)

(b)　\( \ 1 \ \)線当たりの送電端電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(15.2\)　　(2)　\(16.6\)　　(3)　\(28.7\)　　(4)　\(31.8\)　　(5)　\(55.1\)

【ワンポイント解説】

フェランチ効果は深夜等の軽負荷時に受電端電圧が送電端電圧より上昇する現象で，本問はなぜ受電端電圧が高くなるのかを理解するのには最適な問題と言えると思います。ただし，実際の問題としてはフェランチ効果の現象としての問題ではなく回路計算の問題です。

【関連する「電気の神髄」記事】

　　四端子定数のまとめ

【解答】

(a)解答：(2)
問題図の\( \ \pi \ \)形等価回路において，送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \)，受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \)，送電端側のアドミタンスに流れる電流を\( \ {\dot I}_{1} \ \)，受電端側のアドミタンスに流れる電流を\( \ {\dot I}_{2} \ \)とする。

\[
\begin{eqnarray}
{\dot I}_{2} &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] であり，受電端は無負荷であるから，送電端電圧\( \ {\dot E}_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {r}}+\mathrm {j}X{\dot I}_{2} \\[ 5pt ] &=&{\dot E}_{\mathrm {r}}+\mathrm {j}X\left( \mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}}\right) \\[ 5pt ] &=&{\dot E}_{\mathrm {r}}-\frac {XB}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] &=&\left( 1-\frac {XB}{2}\right) {\dot E}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] となる。上式より，\( \ {\dot E}_{\mathrm {s}} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \)は同相であることが分かる。\( \ {\dot E}_{\mathrm {r}} \ \)の式になおし，各値を代入すると，
\[
\begin{eqnarray}
E_{\mathrm {r}}&=&\frac {1}{\displaystyle 1-\frac {XB}{2}}E_{\mathrm {s}} \\[ 5pt ] &=&\frac {1}{\displaystyle 1-\frac {200\times 0.800\times 10^{-3}}{2}}\times \frac {66}{\sqrt {3}} \\[ 5pt ] &=&\frac {1}{\displaystyle 1-0.08}\times \frac {66}{\sqrt {3}} \\[ 5pt ] &≒&1.087\times \frac {66}{\sqrt {3}} \\[ 5pt ] &≒&41.42 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，受電端の線間電圧の大きさ\( \ V_{\mathrm {r}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&\sqrt {3}E_{\mathrm {r}} \\[ 5pt ] &=&\sqrt {3}\times 41.42 \\[ 5pt ] &≒&71.7 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
問題図より，
\[
\begin{eqnarray}
{\dot I}_{2} &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] {\dot I}_{1} &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] であるので，送電端電流\( \ {\dot I}_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}} &=&{\dot I}_{1}+{\dot I}_{2} \\[ 5pt ] &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {s}}+\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] &=&\mathrm {j}\frac {B}{2}\left( {\dot E}_{\mathrm {s}}+{\dot E}_{\mathrm {r}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。(a)より，\( \ {\dot E}_{\mathrm {s}} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \)は同相であることが分かっているので，送電端電流の大きさ\( \ I_{\mathrm {s}} \ \)に各値を代入して求めると，
\[
\begin{eqnarray}
I_{\mathrm {s}} &=&\frac {B}{2}\left( E_{\mathrm {s}}+E_{\mathrm {r}}\right) \\[ 5pt ] &=&\frac {0.800\times 10^{-3}}{2}\times \left( \frac {66}{\sqrt {3}}\times 10^{3}+41.42\times 10^{3}\right) \\[ 5pt ] &=&\frac {0.800\times 10^{-3}}{2}\times \left( 38.11\times 10^{3}+41.42\times 10^{3}\right) \\[ 5pt ] &=&\frac {0.800\times 10^{-3}}{2}\times 79.53\times 10^{3} \\[ 5pt ] &≒&31.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。