Contents
【問題】
【難易度】★★★★☆(やや難しい)
電線\( \ 1 \ \)線の抵抗が\( \ 6 \ \mathrm {\Omega } \ \),誘導性リアクタンスが\( \ 4 \ \mathrm {\Omega } \ \)である三相\( \ 3 \ \)線式送電線について,次の(a)及び(b)の問に答えよ。
(a) 受電端電圧を\( \ 60 \ \mathrm {kV} \ \),送電線での電圧降下率を受電端電圧基準で\( \ 10 \ \mathrm {%} \ \)に保つものとする。この受電端に,力率\( \ 80 \ \mathrm {%} \ \)(遅れ)の負荷を接続する。この場合,受電可能な三相皮相電力の値\( \ \mathrm {[MV\cdot A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 28.9 \ \) (2) \( \ 42.9 \ \) (3) \( \ 50.0 \ \) (4) \( \ 60.5 \ \) (5) \( \ 86.6 \ \)
(b) 受電端に接続する負荷の条件を,遅れ力率\( \ 60 \ \mathrm {%} \ \),三相皮相電力\( \ 65 \ \mathrm {MV\cdot A} \ \)に変更することになった。この場合でも,受電端電圧を\( \ 60 \ \mathrm {kV} \ \),送電線での電圧降下率を受電端電圧基準で\( \ 10 \ \mathrm {%} \ \)に保ちたい。受電端に設置された調相設備から系統に供給すべき無効電力の値\( \ \mathrm {[Mvar]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 12.0 \ \) (2) \( \ 20.5 \ \) (3) \( \ 27.0 \ \) (4) \( \ 31.5 \ \) (5) \( \ 47.1 \ \)
【ワンポイント解説】
受電端に接続可能な皮相電力と力率改善に関する問題です。
電圧降下の近似式を使用するという記載は特にありませんが,各設問の選択肢の差が大きいので,電圧降下の近似式を使用してよいと判断して良いかと思います。
最初はどのように解いたら良いか迷うかと思いますが,図を描いて求められるところを順番に求めていくと解き方の方向性が見えてくるかなと思います。
1.配電線の電圧降下の近似式
本問は送電線ですが,配電線と全く同じ考え方が適用できますので,配電線の単相\( \ 2 \ \)線式及び三相\( \ 3 \ \)線式の電圧降下を紹介します。
①単相\( \ 2 \ \)線式送電線の電圧降下
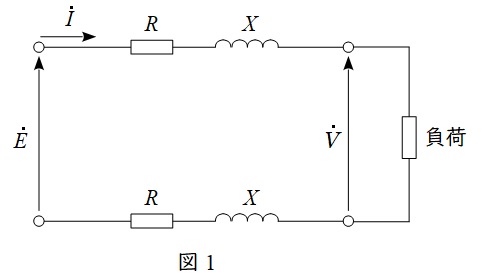
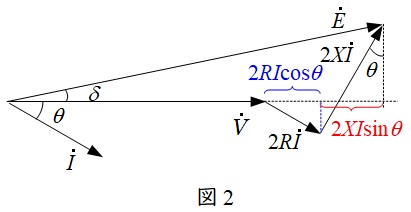
単相\( \ 2 \ \)線式線路は図1のような回路になり,負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって,負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において,\( \ \dot E \ \)と\( \ \dot V \ \)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E&≃&V+2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
E-V&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
\varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
②三相\( \ 3 \ \)線式送電線の電圧降下
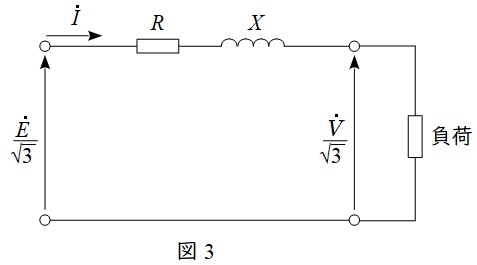
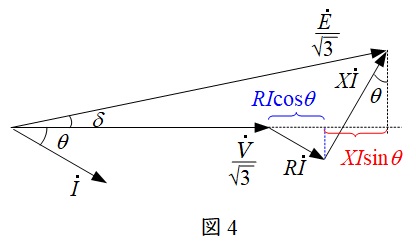
三相回路においては,一相分の等価回路及びベクトル図は図3及び図4のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {E}{\sqrt {3}}&≃&\frac {V}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {E}{\sqrt {3}}-\frac {V}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.線路の有効電力\( \ P \ \)
①単相\( \ 2 \ \)線式
単相\( \ 2 \ \)線式の配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \),線電流が\( \ I \ \mathrm {[A]} \ \),電圧と電流の力率が\( \ \cos \theta \ \)であるとき,送電電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②三相\( \ 3 \ \)線式
三相\( \ 3 \ \)線式の配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \),線電流が\( \ I \ \mathrm {[A]} \ \),電圧と電流の力率が\( \ \cos \theta \ \)であるとき,送電電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(3)
題意に沿って単線図を描くと図5のようになり,各値を図5のようにおく。力率\( \ \cos \theta =0.8 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であり,受電端電圧\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \)基準の電圧降下率\( \ \displaystyle \frac {\varepsilon }{V_{\mathrm {r}}} \ \)が\( \ 10 \ \mathrm {%} \ \)であるから,送電可能な電流値\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\frac {\varepsilon }{V_{\mathrm {r}}}&=&\frac {\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) }{V_{\mathrm {r}}} \\[ 5pt ]
0.1&=&\frac {\sqrt {3}I\times \left( 6\times 0.8 +4\times 0.6 \right) }{60\times 10^{3}} \\[ 5pt ]
I &=&\frac {60\times 10^{3}\times 0.1}{\sqrt {3}\times \left( 6\times 0.8 +4\times 0.6 \right) } \\[ 5pt ]
&≒&481.1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,受電可能な皮相電力\( \ S \ \mathrm {[MV\cdot A]} \ \)は,
\[
\begin{eqnarray}
S&=&\sqrt {3}V_{\mathrm {r}}I \\[ 5pt ]
&=&\sqrt {3}\times 60\times 10^{3}\times 481.1 \\[ 5pt ]
&≒&50.0\times 10^{6} \ \mathrm {[V\cdot A]} → 50.0 \ \mathrm {[MV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
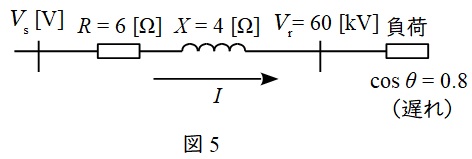
(b)解答:(2)
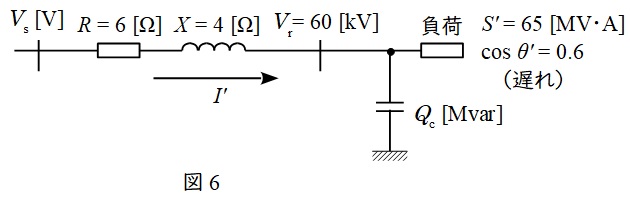
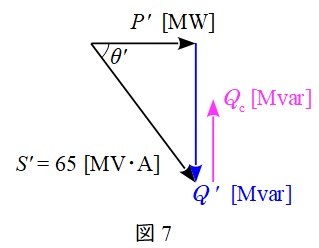
負荷条件変化後,調相設備\( \ Q_{\mathrm {C}} \ \mathrm {[Mvar]} \ \)を接続したときの単線図及びベクトル図を図6及び図7に示す。このとき,
\[
\begin{eqnarray}
\sin \theta ^{\prime }&=&\sqrt {1-\cos ^{2}\theta ^{\prime }} \\[ 5pt ]
&=&\sqrt {1-0.6^{2}} \\[ 5pt ]
&=&0.8 \\[ 5pt ]
P^{\prime }&=&S^{\prime }\cos \theta ^{\prime } \\[ 5pt ]
&=&65\times 0.6 \\[ 5pt ]
&=&39 \ \mathrm {[MW]} \\[ 5pt ]
Q^{\prime }&=&S^{\prime }\sin \theta ^{\prime } \\[ 5pt ]
&=&65\times 0.8 \\[ 5pt ]
&=&52 \ \mathrm {[Mvar]} \\[ 5pt ]
\end{eqnarray}
\]
である。受電端電圧\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \)基準の電圧降下率\( \ \displaystyle \frac {\varepsilon }{V_{\mathrm {r}}} \ \)は,
\[
\begin{eqnarray}
\frac {\varepsilon }{V_{\mathrm {r}}}&=&\frac {\sqrt {3}I^{\prime }\left( R\cos \theta ^{\prime }+X\sin \theta ^{\prime }\right) }{V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,
\[
\begin{eqnarray}
P^{\prime }&=&\sqrt {3}V_{\mathrm {r}}I^{\prime }\cos \theta ^{\prime } \\[ 5pt ]
I^{\prime }\cos \theta ^{\prime }&=&\frac {P^{\prime }}{\sqrt {3}V_{\mathrm {r}}} \\[ 5pt ]
Q^{\prime }&=&\sqrt {3}V_{\mathrm {r}}I^{\prime }\sin \theta ^{\prime } \\[ 5pt ]
I^{\prime }\sin \theta ^{\prime }&=&\frac {Q^{\prime }}{\sqrt {3}V_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
であるので,
\[
\begin{eqnarray}
\frac {\varepsilon }{V_{\mathrm {r}}}&=&\frac {\sqrt {3}I^{\prime }\left( R\cos \theta ^{\prime }+X\sin \theta ^{\prime }\right) }{V_{\mathrm {r}}} \\[ 5pt ]
&=&\frac {\displaystyle \sqrt {3}\left( R\cdot \frac {P^{\prime }}{\sqrt {3}V_{\mathrm {r}}}+X\cdot \frac {Q^{\prime }}{\sqrt {3}V_{\mathrm {r}}}\right) }{V_{\mathrm {r}}} \\[ 5pt ]
&=&\frac {\displaystyle \left( R\cdot \frac {P^{\prime }}{V_{\mathrm {r}}}+X\cdot \frac {Q^{\prime }}{V_{\mathrm {r}}}\right) }{V_{\mathrm {r}}} \\[ 5pt ]
&=&\frac {RP^{\prime }+XQ^{\prime } }{V_{\mathrm {r}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。ここで,調相設備から無効電力\( \ Q_{\mathrm {C}} \ \mathrm {[Mvar]} \ \)を接続したときに電圧降下率が\( \ 10 \ \mathrm {%} \ \)に維持されたとなっていることから,
\[
\begin{eqnarray}
0.1&=&\frac {RP^{\prime }+X\left( Q^{\prime }-Q_{\mathrm {C}}\right) }{V_{\mathrm {r}}^{2}} \\[ 5pt ]
0.1&=&\frac {6\times 39\times 10^{6}+4\times \left( 52\times 10^{6}-Q_{\mathrm {C}}\right) }{\left( 60\times 10^{3}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ Q_{\mathrm {C}} \ \)について解くと,
\[
\begin{eqnarray}
0.1&=&\frac {6\times 39\times 10^{6}+4\times \left( 52\times 10^{6}-Q_{\mathrm {C}}\right) }{\left( 60\times 10^{3}\right) ^{2}} \\[ 5pt ]
6\times 39\times 10^{6}+4\times \left( 52\times 10^{6}-Q_{\mathrm {C}}\right) &=&0.1\times \left( 60\times 10^{3}\right) ^{2} \\[ 5pt ]
234\times 10^{6}+208\times 10^{6}-4Q_{\mathrm {C}} &=&360\times 10^{6} \\[ 5pt ]
4Q_{\mathrm {C}} &=&82\times 10^{6} \\[ 5pt ]
Q_{\mathrm {C}} &=&20.5\times 10^{6} \ \mathrm {[var]} → 20.5 \ \mathrm {[Mvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは