《機械》〈回転機〉[H24:問5]電動機と負荷のトルク特性に関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電動機と負荷のトルク特性の関係について述べたものである。

横軸が回転速度，縦軸がトルクを示す図において\( \ 2 \ \)本の曲線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)は，一方が電動機トルク特性，他方が負荷トルク特性を示している。

いま，曲線\( \ \mathrm {A} \ \)が\( \ \fbox {　 （ア） 　} \ \)特性，曲線\( \ \mathrm {B} \ \)が\( \ \fbox {　 （イ） 　} \ \)特性のときは，\( \ 2 \ \)本の曲線の交点\( \ \mathrm {C} \ \)は不安定な運転点である。これは，何らかの原因で電動機の回転速度がこの点から下降すると，電動機トルクと負荷トルクとの差により電動機が\( \ \fbox {　 （ウ） 　} \ \)されるためである。具体的に，電動機が誘導電動機であり，回転速度に対してトルクが変化しない定トルク特性の負荷のトルクの大きさが，誘導電動機の始動トルクと最大トルクとの間にある場合を考える。このとき，電動機トルクと負荷トルクとの交点は，回転速度零と最大トルクの回転速度との間，及び最大トルクの回転速度と同期速度との間の\( \ 2 \ \)箇所にある。交点\( \ \mathrm {C} \ \)は，\( \ \fbox {　 （エ） 　} \ \)との間の交点に相当する。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 電動機トルク & 負荷トルク & 減　速 & \displaystyle {回転速度零と最大}\atop \displaystyle {トルクの回転速度} \\
\hline
(2) & 電動機トルク & 負荷トルク & 減　速 & \displaystyle {最大トルクの回転}\atop \displaystyle {速度と同期速度} \\
\hline
(3) & 負荷トルク & 電動機トルク & 減　速 & \displaystyle {回転速度零と最大}\atop \displaystyle {トルクの回転速度} \\
\hline
(4) & 負荷トルク & 電動機トルク & 加　速 & \displaystyle {回転速度零と最大}\atop \displaystyle {トルクの回転速度} \\
\hline
(5) & 負荷トルク & 電動機トルク & 加　速 & \displaystyle {最大トルクの回転}\atop \displaystyle {速度と同期速度} \\
\hline
\end{array}
\]

【ワンポイント解説】

誘導電動機のトルク曲線の特性をよく理解していることと，運転点の考え方を理解していないと解けない問題です。文章の読解力も求められる問題なので，2種以上でも出題される可能性がある問題と言えるでしょう。

1.誘導電動機のトルク特性曲線
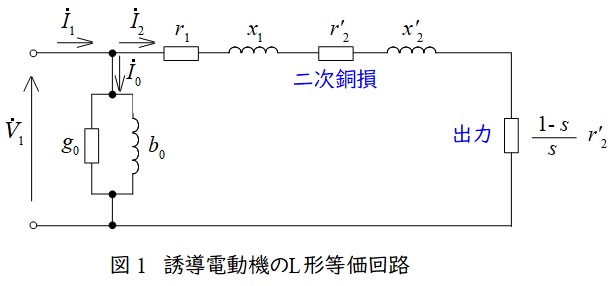
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1の通りであり，トルクは次式で求められます。
（途中の導出は長くなるためここでは割愛します。導出計算は１種の試験でよく出題されます。）
\[
\begin{eqnarray}
T&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] 上式より，\( \ s=1 \)の時始動トルク，\( \ s=0 \ \)の時トルクが零になり，\( \ \displaystyle s_{\mathrm {m}}=\frac {r_{2}^{\prime}}{\sqrt{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}} \ \)の時最大トルク，
\[
\begin{eqnarray}
T_{\mathrm {max}}&=&\frac {3}{2\omega _{s}}\cdot \frac {V_{1}^{2}}{r_{1}+\sqrt{r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
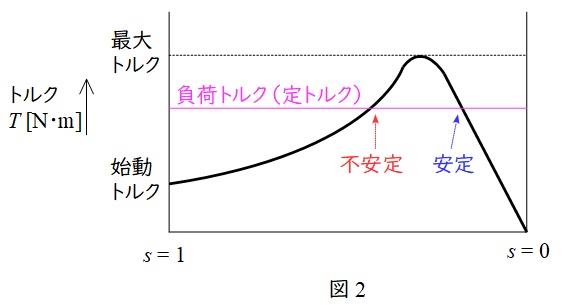
\] が導出され，グラフは図2のようになります。
３種の勉強においては概略波形を知って入れば途中計算は習熟は不要です。始動トルクがあることと概略波形を頭の中に入れておいて下さい。

【解答】

解答：(1)
(ア)
(イ)
(ウ)
曲線\( \ \mathrm {A} \ \)が電動機トルク，曲線\( \ \mathrm {B} \ \)が負荷トルク特性であるとすると，仮に回転数が下がった時，電動機のトルクが小さくなり，負荷のトルクが大きくなり，さらに電動機としては過負荷の状態に移行することになります。そうなると，電動機はさらに減速し，さらに電動機と負荷のトルク差が大きくなります。
一方，曲線\( \ \mathrm {A} \ \)が負荷トルク，曲線\( \ \mathrm {B} \ \)が電動機トルク特性であるとすると，仮に回転数が下がった時，電動機のトルクが大きくなり，負荷のトルクが小さくなります。そうすると，さらに電動機としては軽負荷の状態に移行し，電動機は加速し，元の運転状態に戻ろうとする安定運転となります。
したがって，題意に合うのは（ア）が電動機トルク，（イ）が負荷トルク，（ウ）が減速となります。

(エ)
ワンポイント解説「1.誘導電動機のトルク特性曲線」の図２の通り，定トルク運転時は運転点が２箇所ありますが，不安定な点は，回転速度零と最大トルクの回転速度の間の点となります。