《機械》〈回転機〉[R2:問5]三相同期電動機の力率と誘導起電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図はある三相同期電動機の\( \ 1 \ \)相分の等価回路である。ただし，電機子巻線抵抗は無視している。相電圧\( \ \dot V \ \)の大きさは\( \ V=200 \ \mathrm {V} \ \)，同期リアクタンスは\( \ x_{\mathrm {s}}=8 \ \mathrm {\Omega } \ \)である。この電動機を運転して力率が\( \ 1 \ \)になるように界磁電流を調整したところ，電機子電流\( \ \dot I \ \)の大きさ\( \ I \ \)が\( \ 10 \ \mathrm {A} \ \)になった。このときの誘導起電力\( \ E \ \)の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

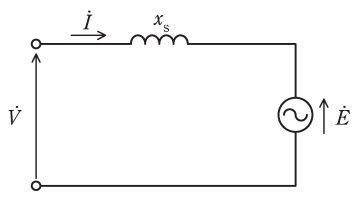
　(1)　\( \ 120 \ \)　　(2)　\( \ 140 \ \)　　(3)　\( \ 183 \ \)　　(4)　\( \ 215 \ \)　　(5)　\( \ 280 \ \)

【ワンポイント解説】

三相同期電動機の各値から誘導起電力を求める問題です。
等価回路が与えられている問題なので，同期電動機の力率\( \ 1 \ \)における電圧及び電流ベクトル図が描けるかどうかが勝負の分かれ目となります。

1.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は，端子電圧\( \ \dot V \ \mathrm {[V]} \ \)，誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)，電機子電流\( \ \dot I \ \mathrm {[A]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。ただし，電機子巻線抵抗は小さいものとします。

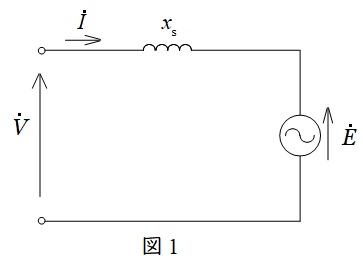
等価回路より，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。
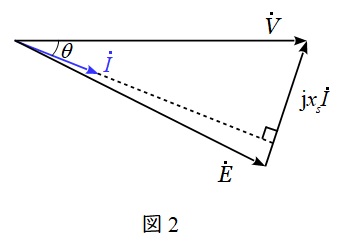
ここで，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \)とすると，ベクトル図は図2のように描くことができます。

【解答】

解答：(4)
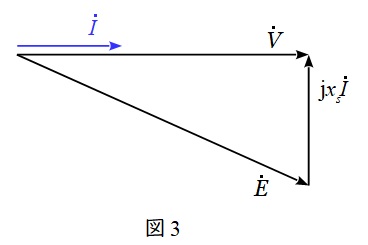
題意より，力率が\( \ 1 \ \)であるから，ベクトル図を描くと図3のようになる。
図3に三平方の定理を適用すると，
\[
\begin{eqnarray}
E^{2} &=& V^{2}+\left( x_{\mathrm {s}} I\right) ^{2} \\[ 5pt ] E &=& \sqrt {V^{2}+\left( x_{\mathrm {s}} I\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
E &=& \sqrt {200^{2}+\left( 8\times 10\right) ^{2}} \\[ 5pt ] &=& \sqrt {46400} \\[ 5pt ] &≒& 215 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。