【問題】
【難易度】★★★☆☆(普通)
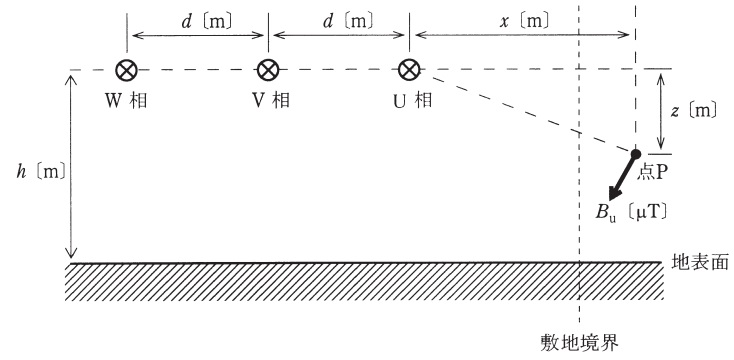
屋外気中絶縁変電所の構内において,図に示すように,地上から\( \ h \ \mathrm {[m]} \ \)の高さに\( \ d \ \mathrm {[m]} \ \)の間隔で母線を設置するとき,変電所周辺での磁束密度が定められた基準値以下であることを確認する手順に関連して,次の問に答えよ。
なお,大地及び変電所の構内の他の設備については考慮しないものとする。
(1) \( \ \mathrm {U} \ \)相母線から水平方向に\( \ x \ \mathrm {[m]} \ \),垂直方向に\( \ z \ \mathrm {[m]} \ \)離れた図中の点\( \ \mathrm {P} \ \)において,磁束密度が基準値以下であることを確認する。このとき,下に示す\( \ \mathrm {U} \ \)相電流\( \ I_{\mathrm {u}} \ \)によって点\( \ \mathrm {P} \ \)に生じる磁束密度\( \ B_{\mathrm {u}} \ \mathrm {[\mu T]} \ \)を,\( \ x \ \),\( \ z \ \),\( \ I \ \),\( \ \omega \ \),\( \ t \ \)を用いて表せ。ただし,母線は無限長の直線導体とみなし,導体の太さは無視する。また,導体から点\( \ \mathrm {P} \ \)までの空間の透磁率は\( \ \mu =4\pi \times 10^{-7} \ \mathrm {[H / m]} \ \)で一様とする。
電流 \( \ \mathrm {U} \ \)相 \( \ I_{\mathrm {u}}=\sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) \ \mathrm {[A]} \ \)
\( \ \mathrm {V} \ \)相 \( \ I_{\mathrm {v}}=\sqrt {2}I\sin \omega t \ \mathrm {[A]} \ \)
\( \ \mathrm {W} \ \)相 \( \ I_{\mathrm {w}}=\sqrt {2}I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) \ \mathrm {[A]} \ \)
\( \left( I \ \mathrm {[A]} \right. \):電流実効値,\( \ \omega \ \mathrm {[rad / s]} \ \):角周波数,\( \ t \ \mathrm {[s]} \ \):時間\( \left. \right) \ \)
※ 電流の向きは,図において紙面の表から裏に向かう方向を正とする。
(2) 各相の電流によって点\( \ \mathrm {P} \ \)に生じる磁束密度の合成値\( \ B \ \mathrm {[\mu T]} \ \)を\( \ x \ \),\( \ z \ \),\( \ d \ \),\( \ I \ \),\( \ \omega \ \),\( \ t \ \)を用いて表せ。
(3) 絶縁に問題がないとした場合,母線の間隔\( \ d \ \mathrm {[m]} \ \)を小さくしていくと,磁束密度の合成値\( \ B \ \mathrm {[\mu T]} \ \)はどのような値に近づくかを,(2)で求めた式から導出せよ。なお,\( \ x \ \)は\( \ d \ \)に対して十分大きい値とする。
(4) 磁束密度の測定点\( \ \mathrm {P} \ \)を固定とし,さらに母線の間隔\( \ d \ \mathrm {[m]} \ \)の値を固定した条件において,測定される磁束密度を低減する方策を二つ挙げ,簡潔に説明せよ。ただし,磁界を遮へいする方策は考慮しないものとする。
【ワンポイント解説】
変電所周辺の磁束密度の大きさを求める計算問題です。
公式自体は難解な公式を使用しませんが,(2)の計算がやや複雑となり,(2)が解ければ,(3)と(4)がそれほど時間を要せず解けるので,点数差が開きやすい問題と言えます。
\( \ 1 \ \)種二次試験では高い計算能力が求められますが,本問程度であれば標準問題の範囲内となりますので,確実に導出できるようになりましょう。
1.アンペア(アンペール)の周回積分の法則
空間上の磁界ベクトルを\( \ \boldsymbol H \ \),\( \ \mathrm {C} \ \)を閉曲線,\( \ \mathrm {d}\boldsymbol l \ \)を\( \ \mathrm {C} \ \)上の微小区間ベクトル,\( \ I \ \)を\( \ \mathrm {C} \ \)と鎖交する電流の総量とすると,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,これをアンペアの周回積分の法則といいます。
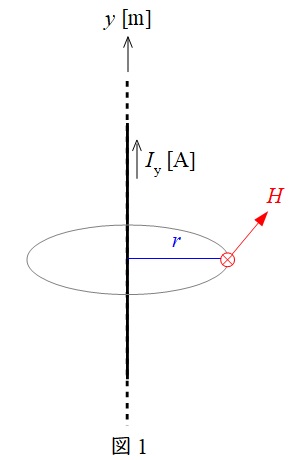
例えば,図1のように無限長直線電流\( \ I_{\mathrm {y}} \ \)が流れているとき,電線から距離\( \ r \ \)の位置での磁界の強さ\( \ H \ \)は,\( \ l=2\pi r \ \)なので,
\[
\begin{eqnarray}
2\pi r H&=&I_{\mathrm {y}} \\[ 5pt ]
H&=&\frac {I_{\mathrm {y}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)\( \ \mathrm {U} \ \)相電流\( \ I_{\mathrm {u}} \ \)によって点\( \ \mathrm {P} \ \)に生じる磁束密度\( \ B_{\mathrm {u}} \ \mathrm {[\mu T]} \ \)
\( \ \mathrm {U} \ \)相母線から点\( \ \mathrm {P} \ \)までの距離\( \ r_{\mathrm {u}} \ \)は,三平方の定理より,
\[
\begin{eqnarray}
r_{\mathrm {u}}&=&\sqrt {x^{2}+z^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「1.アンペア(アンペール)の周回積分の法則」より,\( \ \mathrm {U} \ \)相電流\( \ I_{\mathrm {u}} \ \)による点\( \ \mathrm {P} \ \)での磁界の強さ\( \ H_{\mathrm {u}} \ \)は,
\[
\begin{eqnarray}
H_{\mathrm {u}}&=&\frac {I_{\mathrm {u}}}{2\pi r_{\mathrm {u}}} \\[ 5pt ]
&=&\frac {I_{\mathrm {u}}}{2\pi \sqrt {x^{2}+z^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,磁束密度\( \ B_{\mathrm {u}} \ \)は,
\[
\begin{eqnarray}
B_{\mathrm {u}}&=&\mu H_{\mathrm {u}} \\[ 5pt ]
&=&\frac {\mu I_{\mathrm {u}}}{2\pi \sqrt {x^{2}+z^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ I_{\mathrm {u}}=\sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) \ \),\( \ \mu =4\pi \times 10^{-7} \ \mathrm {[H / m]} \ \)を代入すると,
\[
\begin{eqnarray}
B_{\mathrm {u}}&=&\frac {\mu I_{\mathrm {u}}}{2\pi \sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {4\pi \times 10^{-7}\times \sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{2\pi \sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {2 \sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{\sqrt {x^{2}+z^{2}}}\times 10^{-7} \ \mathrm {[T]} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {x^{2}+z^{2}}} \ \mathrm {[\mu T]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)各相の電流によって点\( \ \mathrm {P} \ \)に生じる磁束密度の合成値\( \ B \ \mathrm {[\mu T]} \ \)
\( \ \mathrm {V} \ \)相電流\( \ I_{\mathrm {v}} \ \)及び\( \ \mathrm {W} \ \)相電流\( \ I_{\mathrm {w}} \ \)によって点\( \ \mathrm {P} \ \)に生じる磁束密度\( \ B_{\mathrm {v}} \ \)及び\( \ B_{\mathrm {w}} \ \)は,\( \ x→x+d \ \)及び\( \ x→x+2d \ \)として,各電流の値を代入すれば良いので,
\[
\begin{eqnarray}
B_{\mathrm {v}}&=&\frac {\sqrt {2}I\sin \omega t}{5\sqrt {\left( x+ d \right) ^{2}+z^{2}}} \\[ 5pt ]
B_{\mathrm {w}}&=&\frac {\sqrt {2}I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,それぞれの水平方向\( \ \left( x \right) \ \)成分及び垂直方向\( \ \left( y \right) \ \)成分は,
\[
\begin{eqnarray}
B_{\mathrm {ux}}&=&B_{\mathrm {u}}\cdot \frac {z}{\sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {x^{2}+z^{2}}}\cdot \frac {z}{\sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}zI\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\left( x^{2}+z^{2}\right) } \\[ 5pt ]
B_{\mathrm {uy}}&=&B_{\mathrm {u}}\cdot \frac {x}{\sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {x^{2}+z^{2}}}\cdot \frac {x}{\sqrt {x^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}xI\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\left( x^{2}+z^{2}\right) } \\[ 5pt ]
B_{\mathrm {vx}}&=&B_{\mathrm {v}}\cdot \frac {z}{\sqrt {\left( x+ d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \omega t }{5\sqrt {\left( x+ d \right) ^{2}+z^{2}}}\cdot \frac {z}{\sqrt {\left( x+ d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}zI\sin \omega t }{5\left\{ \left( x+ d \right) ^{2}+z^{2}\right\} } \\[ 5pt ]
B_{\mathrm {vy}}&=&B_{\mathrm {v}}\cdot \frac {x+d}{\sqrt {\left( x+ d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \omega t }{5\sqrt {\left( x+ d \right) ^{2}+z^{2}}}\cdot \frac {x+ d}{\sqrt {\left( x+ d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}\left( x+ d \right) I\sin \omega t }{5\left\{ \left( x+ d \right) ^{2}+z^{2}\right\} } \\[ 5pt ]
B_{\mathrm {wx}}&=&B_{\mathrm {w}}\cdot \frac {z}{\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}}\cdot \frac {z}{\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}zI\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\left\{ \left( x+ 2d \right) ^{2}+z^{2}\right\} } \\[ 5pt ]
B_{\mathrm {wy}}&=&B_{\mathrm {w}}\cdot \frac {x+ 2d}{\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}}\cdot \frac {x+ 2d}{\sqrt {\left( x+ 2d \right) ^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {2}\left( x+ 2d \right) I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\left\{ \left( x+ 2d \right) ^{2}+z^{2}\right\} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,磁束密度の合成値\( \ B \ \)は,
\[
\begin{eqnarray}
B&=&\sqrt {\left( B_{\mathrm {ux}}+B_{\mathrm {vx}}+B_{\mathrm {wx}}\right) ^{2}+\left( B_{\mathrm {uy}}+B_{\mathrm {vy}}+B_{\mathrm {wy}}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\left[ \frac {\sqrt {2}zI\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\left( x^{2}+z^{2}\right) }+\frac {\sqrt {2}zI\sin \omega t }{5\left\{ \left( x+ d \right) ^{2}+z^{2}\right\} }+\frac {\sqrt {2}zI\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\left\{ \left( x+ 2d \right) ^{2}+z^{2}\right\} }\right] ^{2}+\left[ \frac {\sqrt {2}xI\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{5\left( x^{2}+z^{2}\right) }+\frac {\sqrt {2}\left( x+ d \right) I\sin \omega t }{5\left\{ \left( x+ d \right) ^{2}+z^{2}\right\} }+\frac {\sqrt {2}\left( x+ 2d \right) I\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{5\left\{ \left( x+ 2d \right) ^{2}+z^{2}\right\} }\right] ^{2}} \\[ 5pt ]
&=&\frac {\sqrt {2}}{5}I\sqrt {z^{2}\left\{ \frac {\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }+\frac {\sin \omega t }{ \left( x+ d \right) ^{2}+z^{2} }+\frac {\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ \left( x+ 2d \right) ^{2}+z^{2} }\right\} ^{2}+\left\{ \frac {x\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }+\frac {\left( x+ d \right) \sin \omega t }{ \left( x+ d \right) ^{2}+z^{2} }+\frac {\left( x+ 2d \right) \sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ \left( x+ 2d \right) ^{2}+z^{2} }\right\} ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)母線の間隔\( \ d \ \mathrm {[m]} \ \)を小さくしていくと,磁束密度の合成値\( \ B \ \mathrm {[\mu T]} \ \)はどのような値に近づくか
(2)の解答式に\( \ x≫d \ \)を適用すると,
\[
\begin{eqnarray}
B&=&\frac {\sqrt {2}}{5}I\sqrt {z^{2}\left\{ \frac {\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }+\frac {\sin \omega t }{ \left( x+ 0 \right) ^{2}+z^{2} }+\frac {\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ \left( x+ 2\times 0 \right) ^{2}+z^{2} }\right\} ^{2}+\left\{ \frac {x\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }+\frac {\left( x+ 0 \right) \sin \omega t }{ \left( x+ 0 \right) ^{2}+z^{2} }+\frac {\left( x+ 2\times 0 \right) \sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ \left( x+ 2\times 0 \right) ^{2}+z^{2} }\right\} ^{2}} \\[ 5pt ]
&=&\frac {\sqrt {2}}{5}I\sqrt {z^{2}\left\{ \frac {\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) + \sin \omega t +\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }\right\} ^{2}+x^{2}\left\{ \frac {\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) + \sin \omega t +\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }\right\} ^{2}} \\[ 5pt ]
&=&\frac {\sqrt {2}}{5}I\sqrt {\left( x^{2}+z^{2}\right) \left\{ \frac {\sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) + \sin \omega t +\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) }{ x^{2}+z^{2} }\right\} ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle \sin \left( \omega t -\displaystyle \frac {2\pi }{3} \right) + \sin \omega t +\sin \left( \omega t +\displaystyle \frac {2\pi }{3} \right) =0 \ \)であることから,磁束密度の合成値\( \ B \ \mathrm {[\mu T]} \ \)は\( \ d \ \mathrm {[m]} \ \)を小さくしていくと零に近づいていくことがわかる。
(4)測定される磁束密度を低減する方策を二つ挙げ,簡潔に説明
(3)より,\( \ x≫d \ \)とする又は各母線からの距離を等しくすることが望ましいが,「磁束密度の測定点\( \ \mathrm {P} \ \)を固定とし,さらに母線の間隔\( \ d \ \mathrm {[m]} \ \)の値を固定した条件」となっているので,磁束密度を低減する方策は以下の方策が挙げられる。
・母線の設置位置を変更(水平方向の位置変更又はかさ上げ)することにより,点\( \ \mathrm {P} \ \)との間の距離を大きくする。
・母線の電線配列を三角配列に変更することにより,磁界の打ち消し効果を高める。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん