【問題】
【難易度】★★★☆☆(普通)
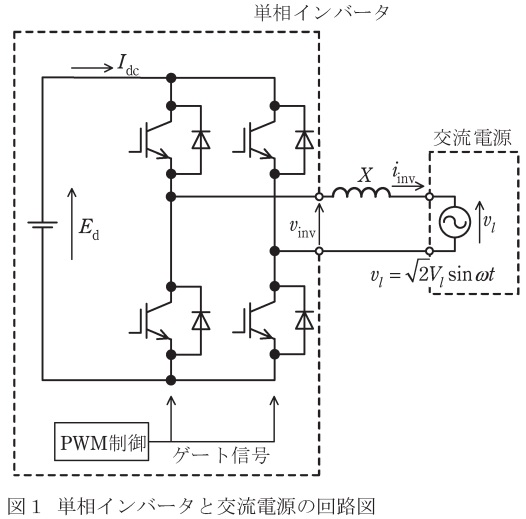
図1にはリアクトルを介して交流電源に連系する単相インバータを示す。インバータに三角波比較正弦波変調\( \ \mathrm {PWM} \ \)制御を適用する。この間では高調波を無視し,インバータの出力電圧の基本波瞬時値を\( \ v_{\mathrm {inv}}=\sqrt {2}V_{\mathrm {inv}}\sin \left( \omega t +\varphi \right) \ \mathrm {[V]} \ \)とする。ここで,\( \ V_{\mathrm {inv}} \ \)は変調率\( \ k \ \)(ただし,\( \ 0≦k≦1 \ \))のときに出力する交流電圧の基本波実効値,\( \ \omega \ \)は交流電源電圧の角周波数,\( \ \varphi \ \)は交流電源電圧の位相を基準とした\( \ v_{\mathrm {inv}} \ \)の位相角である。また,直流電源である電池電圧\( \ E_{\mathrm {d}} \ \)の初期値は,\( \ E_{\mathrm {d0}}=200 \ \mathrm {V} \ \),リアクトルのリアクタンスは\( \ X=0.75 \ \mathrm {\Omega } \ \)で,回路の抵抗分は無視できるものとする。さらに,交流電源の実効値電圧は\( \ V_{l}=100 \ \mathrm {V} \ \)とする。この回路の動作に関して,次の問に答えよ。
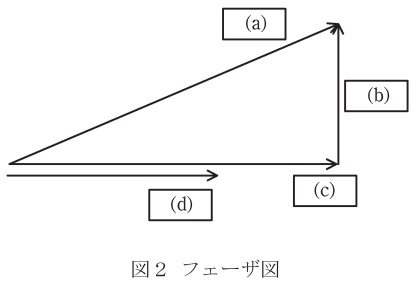
(1) インバータは,交流電源に力率\( \ 1 \ \)の有効電力を供給している。このときのフェーザ図を図2に示す。図中の(a)~(d)のフェーザは何のフェーザであるかを示せ。ただし,その内三つは,インバータ出力電圧\( \ {\dot V}_{\mathrm {inv}} \ \),インバータ出力電流\( \ {\dot I}_{\mathrm {inv}} \ \),交流電源電圧\( \ {\dot V}_{l} \ \)のフェーザである。
(2) 交流電源には力率\( \ 1 \ \)で\( \ 10 \ \mathrm {kW} \ \)の有効電力が供給されている。電池電圧\( \ E_{\mathrm {d}}=E_{\mathrm {d0}} \ \)一定と仮定して,次の値を示せ。
・インバータの出力電圧\( \ v_{\mathrm {inv}} \ \)の実効値\( \ V_{\mathrm {inv}} \ \)
・インバータが出力する皮相電力\( \ S \ \),無効電力\( \ Q \ \)
・電池に流れる直流電流平均値\( \ I_{\mathrm {dc}} \ \)
・\( \ \mathrm {PWM} \ \)制御の変調率\( \ k \ \)
(3) 電池は放電が進むと電池電圧\( \ E_{\mathrm {d}} \ \)が低下することが一般的である。変調率が\( \ 0≦k≦1 \ \)の範囲で小問(2)の交流電圧を出力できる電池電圧\( \ E_{\mathrm {d}} \ \)の最小値は\( \ E_{\mathrm {d0}} \ \)に対して何%であるかを示せ。
【ワンポイント解説】
単相インバータと\( \ \mathrm {PWM} \ \)制御に関する問題です。
本問においては単相インバータの細かなスイッチ動作や\( \ \mathrm {PWM} \ \)制御の関連の知識は必須ではありませんが,メカニズムを理解すると様々な問題に応用できるので,理解しておいた方と良いかと思います。
1.単相\( \ \mathrm {PWM} \ \)インバータの動作
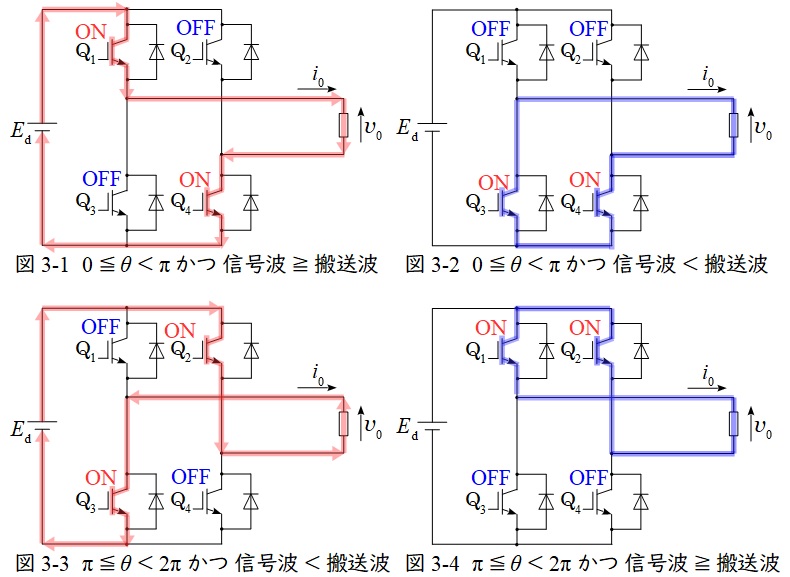
図3-1~図3-4に示すように,単相\( \ \mathrm {PWM} \ \)インバータは信号波と搬送波の大小比較によりスイッチ\( \ \mathrm {Q}_{1} \ \)と\( \ \mathrm {Q}_{3} \ \)を,位相により\( \ \mathrm {Q}_{2} \ \)と\( \ \mathrm {Q}_{4} \ \)をオンオフ制御することにより,出力のパルス幅を制御することで,交流電力を得る方法です。
ここでは簡単に出力が純抵抗であり,回路の損失やリプルがない理想的な場合を例を示します。
①\( \ 0≦\theta < \pi \ \)かつ信号波≧搬送波のとき
スイッチ\( \ \mathrm {Q}_{1} \ \)と\( \ \mathrm {Q}_{4} \ \)をオンとし,出力電圧は\( \ E_{\mathrm {d}} \ \)となります。
②\( \ 0≦\theta < \pi \ \)かつ信号波<搬送波のとき
スイッチ\( \ \mathrm {Q}_{3} \ \)と\( \ \mathrm {Q}_{4} \ \)をオンとし,出力電圧は\( \ 0 \ \)となります。
③\( \ \pi ≦\theta < 2\pi \ \)かつ信号波<搬送波のとき
スイッチ\( \ \mathrm {Q}_{3} \ \)と\( \ \mathrm {Q}_{2} \ \)をオンとし,出力電圧は\( \ -E_{\mathrm {d}} \ \)となります。
④\( \ \pi ≦\theta < 2\pi \ \)かつ信号波≧搬送波のとき
スイッチ\( \ \mathrm {Q}_{1} \ \)と\( \ \mathrm {Q}_{2} \ \)をオンとし,出力電圧は\( \ 0 \ \)となります。
2.\( \ \mathrm {PWM} \ \)制御と変調率
\( \ \mathrm {PWM} \ \)制御は出力電圧を交流電源の搬送波と信号波の大きさの比較により行います。
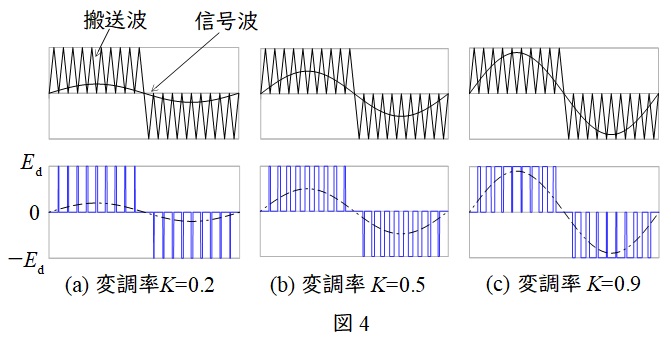
図3の単相インバータの出力例は図4のようになります。
変調率は搬送波と信号波の振幅の比率をいい,図4のように変調率\( \ K \ \)を\( \ 0 \ \)から\( \ 1 \ \)まで変化させることで出力電圧の波高値を\( \ 0 \ \)から\( \ E_{\mathrm {d}} \ \)まで制御することができ,変調率に比例した出力電圧を得ることができます。
【関連する「電気の神髄」記事】
【解答】
(1)図中の(a)~(d)のフェーザは何のフェーザであるか
図1より,インバータの交流出力の関係式は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {inv}} &=&{\dot V}_{l}+\mathrm {j}X{\dot I}_{\mathrm {inv}} \\[ 5pt ]
\end{eqnarray}
\]
となり,交流電源に力率\( \ 1 \ \)の有効電力を供給しているので,\( \ {\dot V}_{l} \ \)と\( \ {\dot I}_{\mathrm {inv}} \ \)は同相である。
したがって,(a)\( \ {\dot V}_{\mathrm {inv}} \ \),(b)\( \ \mathrm {j}X{\dot I}_{\mathrm {inv}} \ \),(c)\( \ {\dot V}_{l} \ \),(d)\( \ {\dot I}_{\mathrm {inv}} \ \)と求められる。
(2)電池電圧\( \ E_{\mathrm {d}}=E_{\mathrm {d0}} \ \)一定と仮定して各値を示す
・インバータの出力電圧\( \ v_{\mathrm {inv}} \ \)の実効値\( \ V_{\mathrm {inv}} \ \)
交流電源には力率\( \ 1 \ \)で\( \ P=10 \ \mathrm {[kW]} \ \)の有効電力が供給されているので,\( \ {\dot I}_{\mathrm {inv}} \ \)の大きさ\( \ I_{\mathrm {inv}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {inv}} &=&\frac {P}{V_{l}} \\[ 5pt ]
&=&\frac {10\times 10^{3}}{100} \\[ 5pt ]
&=&100 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
である。これより,インバータの出力電圧\( \ v_{\mathrm {inv}} \ \)の実効値\( \ V_{\mathrm {inv}} \ \)は,図2に三平方の定理を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {inv}} &=&\sqrt {V_{l}^{2}+\left( XI_{\mathrm {inv}}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {100^{2}+\left( 0.75 \times 100 \right) ^{2}} \\[ 5pt ]
&=&125 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
・インバータが出力する皮相電力\( \ S \ \),無効電力\( \ Q \ \)
インバータが出力する皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)は,
\[
\begin{eqnarray}
S &=&V_{\mathrm {inv}}I_{\mathrm {inv}} \\[ 5pt ]
&=&125\times 100 \\[ 5pt ]
&=&12 \ 500 \ \mathrm {[V\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,無効電力\( \ Q \ \)は,
\[
\begin{eqnarray}
Q &=&\sqrt {S^{2}-P^{2}} \\[ 5pt ]
&=&\sqrt {12 \ 500^{2}-\left( 10\times 10^{3}\right) ^{2}}\\[ 5pt ]
&=&7 \ 500 \ \mathrm {[var]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
・電池に流れる直流電流平均値\( \ I_{\mathrm {dc}} \ \)
回路の抵抗分は無視できるので,電源が供給する電力と交流電源に供給される電力は等しい。したがって,直流電流平均値\( \ I_{\mathrm {dc}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d0}}I_{\mathrm {dc}} &=&P \\[ 5pt ]
I_{\mathrm {dc}} &=&\frac {P}{E_{\mathrm {d0}}} \\[ 5pt ]
&=&\frac {10\times 10^{3}}{200} \\[ 5pt ]
&=&50 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
・\( \ \mathrm {PWM} \ \)制御の変調率\( \ k \ \)
ワンポイント解説「2.\( \ \mathrm {PWM} \ \)制御と変調率」の通り,インバータ出力電圧の波高値(最大値)\( \ V_{\mathrm {m}}=\sqrt {2}V_{\mathrm {inv}} \ \)は変調率\( \ k \ \)と電池電圧\( \ E_{\mathrm {d}} \ \)の積で求められるので,
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&kE_{\mathrm {d}} \\[ 5pt ]
\sqrt {2}V_{\mathrm {inv}} &=&kE_{\mathrm {d}} \\[ 5pt ]
k&=&\frac {\sqrt {2}V_{\mathrm {inv}}}{E_{\mathrm {d}}} \\[ 5pt ]
&=&\frac {\sqrt {2}\times 125}{200} \\[ 5pt ]
&≒&0.88388 → 0.884 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)交流電圧を出力できる電池電圧\( \ E_{\mathrm {d}} \ \)の最小値は\( \ E_{\mathrm {d0}} \ \)に対して何%であるか
ワンポイント解説「2.\( \ \mathrm {PWM} \ \)制御と変調率」の通り,交流電圧を出力できる電池電圧\( \ E_{\mathrm {d}} \ \)の最小値\( \ E_{\mathrm {dmin}} \ \)は,変調率\( \ k=1 \ \)の時の値であるから,
\[
\begin{eqnarray}
kE_{\mathrm {d}}&=&V_{\mathrm {m}} \\[ 5pt ]
E_{\mathrm {dmin}}&=&\sqrt {2}V_{\mathrm {inv}} \\[ 5pt ]
&=&\sqrt {2}\times 125 \\[ 5pt ]
&≒&176.78 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ E_{\mathrm {dmin}} \ \)と\( \ E_{\mathrm {d0}} \ \)の比は,
\[
\begin{eqnarray}
\frac {E_{\mathrm {dmin}}}{E_{\mathrm {d0}}}&=&\frac {176.78}{200} \\[ 5pt ]
&=&0.8839 → 88.4 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん