【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直流回路の合成抵抗に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
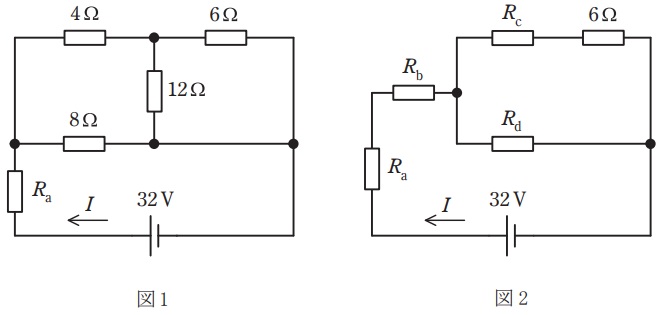
図1において,電源側から見た回路全体の合成抵抗\( \ R \ \)を求めたい。なお,抵抗\( \ R_{\mathrm {a}} \ \)は\( \ 60 \ \mathrm {W} \ \)の電力を消費しており,\( \ 5 \ \mathrm {\Omega } \ \)より小さいことが分かっている。
まず,抵抗\( \ 4 \ \mathrm {\Omega } \ \),\( \ 8 \ \mathrm {\Omega } \ \)及び\( \ 12 \ \mathrm {\Omega } \ \)からなる\( \ \Delta \ \)形抵抗に対して\( \ \mathrm {\Delta -Y} \ \)変換を施し,図2の等価回路に変換すると,\( \ R_{\mathrm {b}}= \ \fbox { (1) } \ \mathrm {\Omega } \ \),\( \ R_{\mathrm {c}}= \ \fbox { (2) } \ \mathrm {\Omega } \ \),\( \ R_{\mathrm {d}}= \ \fbox { (3) } \ \mathrm {\Omega } \ \)が得られる。
次に,\( \ R \ \)は,回路を流れる電流\( \ I \ \)と電源電圧から得られるので,\( \ I \ \)を求めることとする。
\( \ I \ \)を求めると,\( \ I= \ \fbox { (4) } \ \mathrm {A} \ \)となる。したがって,電源側から見た回路全体の合成抵抗は,\( \ R= \ \fbox { (5) } \ \mathrm {\Omega } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {4}{3} &(ロ)& 2.4 &(ハ)& 6.4 \\[ 5pt ]
&(ニ)& \frac {3}{4} &(ホ)& \frac {1}{3} &(ヘ)& 4 \\[ 5pt ]
&(ト)& \frac {2}{3} &(チ)& 3 &(リ)& 8 \\[ 5pt ]
&(ヌ)& 3.2 &(ル)& 2 &(ヲ)& 10 \\[ 5pt ]
&(ワ)& 12 &(カ)& 5 &(ヨ)& 6 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ \mathrm {\Delta -Y} \ \)変換を含む直流回路の合成抵抗の導出に関する問題です。
(4)が少し特殊な解き方ですが,受験生のレベルを考えると多くの受験生が解いてくると予想されますので,確実に理解するようにして下さい。
不平衡負荷の\( \ \mathrm {\Delta -Y} \ \)変換が必要な問題は\( \ 1 \ \)種では毎年のように出題されているので,必ずマスターしておきましょう。
1.不平衡負荷の\( \ \mathrm {\Delta – Y} \ \)変換と\( \ \mathrm {Y – \Delta} \ \)変換
a.\( \ \mathrm {\Delta – Y} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
b.\( \ \mathrm {Y – \Delta} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]

2.二次方程式の解の公式
\( \ x \ \)に関する二次方程式\( \ ax^{2}+bx+c=0 \ \)の解は,
\[
\begin{eqnarray}
x &=&\frac {-b±\sqrt {b^{2}-4ac}}{2a} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,仮に\( \ b=2B \ \)と表すことができる場合には,二次方程式\( \ ax^{2}+2Bx+c=0 \ \)の解は,
\[
\begin{eqnarray}
x &=&\frac {-B±\sqrt {B^{2}-ac}}{a} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:イ
図1の\( \ 4 \ \mathrm {\Omega } \ \),\( \ 8 \ \mathrm {\Omega } \ \),\( \ 12 \ \mathrm {\Omega } \ \)の抵抗を\( \ \mathrm {\Delta – Y} \ \)変換して\( \ R_{\mathrm {b}} \ \)を求めると,ワンポイント解説「1.不平衡負荷の\( \ \mathrm {\Delta – Y} \ \)変換と\( \ \mathrm {Y – \Delta} \ \)変換」の通り,
\[
\begin{eqnarray}
R_{\mathrm {b}} &=& \frac {4\times 8}{4+8+12} \\[ 5pt ]
&=& \frac {4}{3} \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ル
(1)と同様に,図1の\( \ 4 \ \mathrm {\Omega } \ \),\( \ 8 \ \mathrm {\Omega } \ \),\( \ 12 \ \mathrm {\Omega } \ \)の抵抗を\( \ \mathrm {\Delta – Y} \ \)変換して\( \ R_{\mathrm {c}} \ \)を求めると,
\[
\begin{eqnarray}
R_{\mathrm {c}} &=& \frac {4\times 12}{4+8+12} \\[ 5pt ]
&=& 2 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
(1),(2)と同様に,図1の\( \ 4 \ \mathrm {\Omega } \ \),\( \ 8 \ \mathrm {\Omega } \ \),\( \ 12 \ \mathrm {\Omega } \ \)の抵抗を\( \ \mathrm {\Delta – Y} \ \)変換して\( \ R_{\mathrm {d}} \ \)を求めると,
\[
\begin{eqnarray}
R_{\mathrm {d}} &=& \frac {8\times 12}{4+8+12} \\[ 5pt ]
&=& 4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:カ
\( \ \displaystyle R_{\mathrm {b}}=\frac {4}{3} \ \mathrm {[\Omega ]} \ \),\( \ \displaystyle R_{\mathrm {c}}=2 \ \mathrm {[\Omega ]} \ \),\( \ \displaystyle R_{\mathrm {d}}=4 \ \mathrm {[\Omega ]} \ \),\( \ 6 \ \mathrm {\Omega } \ \)の合成抵抗\( \ R^{\prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R^{\prime } &=& R_{\mathrm {b}}+\frac {\left( R_{\mathrm {c}}+6\right) R_{\mathrm {d}}}{\left( R_{\mathrm {c}}+6\right) +R_{\mathrm {d}}} \\[ 5pt ]
&=& \frac {4}{3}+\frac {\left( 2+6\right) \times 4}{\left( 2+6\right) +4} \\[ 5pt ]
&=& 4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,回路を流れる電流\( \ I \ \)は,
\[
\begin{eqnarray}
I &=& \frac {32}{R_{\mathrm {a}}+R^{\prime }} \\[ 5pt ]
&=& \frac {32}{R_{\mathrm {a}}+4} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ R_{\mathrm {a}} \ \)での消費電力\( \ P_{\mathrm {a}}=60 \ \mathrm {[W]} \ \)を求める式より,
\[
\begin{eqnarray}
P_{\mathrm {a}} &=& R_{\mathrm {a}}I^{2} \\[ 5pt ]
60&=& R_{\mathrm {a}}\left( \frac {32}{R_{\mathrm {a}}+4}\right) ^{2} \\[ 5pt ]
&=& \frac {1024R_{\mathrm {a}}}{R_{\mathrm {a}}^{2}+8R_{\mathrm {a}}+16} \\[ 5pt ]
60R_{\mathrm {a}}^{2}+480R_{\mathrm {a}}+960&=&1024R_{\mathrm {a}} \\[ 5pt ]
60R_{\mathrm {a}}^{2}-544R_{\mathrm {a}}+960&=&0 \\[ 5pt ]
15R_{\mathrm {a}}^{2}-136R_{\mathrm {a}}+240&=&0 \\[ 5pt ]
R_{\mathrm {a}}&=&\frac {68±\sqrt {68^{2}-15\times 240}}{15} \\[ 5pt ]
&≒&2.4,6.67 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ R_{\mathrm {a}} \ \)が\( \ 5 \ \mathrm {\Omega } \ \)より小さいことが分かっているので,\( \ R_{\mathrm {a}}=2.4 \ \mathrm {[\Omega ]} \ \)と求められる。したがって,回路を流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {32}{R_{\mathrm {a}}+4} \\[ 5pt ]
&=& \frac {32}{2.4+4} \\[ 5pt ]
&=& 5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
回路全体の合成抵抗\( \ \displaystyle R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R &=& R_{\mathrm {a}}+R^{\prime } \\[ 5pt ]
&=& 2.4+4 \\[ 5pt ]
&=& 6.4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん