《理論》〈電気回路〉[H22:問5]中性線を含む不平衡三相交流回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，三相回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な式を解答群の中から選びなさい。

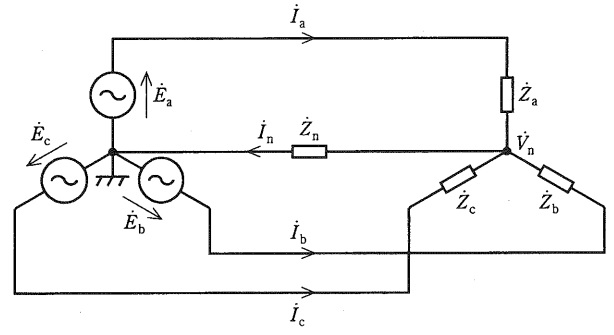
図の非対称三相\( \ \mathrm {Y} \ \)形負荷回路で，\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)各相のインピーダンスをそれぞれ\( \ {\dot Z}_{\mathrm {a}}=10 \ \mathrm {[\Omega ]} \ \)，\( \ {\dot Z}_{\mathrm {b}}=12.5 \ \mathrm {[\Omega ]} \ \)，\( \ {\dot Z}_{\mathrm {c}}=16 \ \mathrm {[\Omega ]} \ \)，負荷中性点と接地点間のインピーダンスを\( \ {\dot Z}_{\mathrm {n}}=5 \ \mathrm {[\Omega ]} \ \)とする。この負荷に\( \ {\dot E}_{\mathrm {a}}=100 \ \mathrm {[V]} \ \)，\( \ \displaystyle {\dot E}_{\mathrm {b}}=100∠-\frac {2\pi }{3} \ \mathrm {[V]} \ \)，\( \ \displaystyle {\dot E}_{\mathrm {c}}=100∠-\frac {4\pi }{3} \ \mathrm {[V]} \ \)の対称三相\( \ \mathrm {Y} \ \)形電源を接続した。ただし，電源の中性点は接地されているものとする。このとき，負荷中性点の電圧\( \ {\dot V}_{\mathrm {n}} \ \)は\( \ \fbox {　 （１） 　} \ \mathrm {[V]} \ \)であり，流れる各線電流はそれぞれ\( \ {\dot I}_{\mathrm {a}}= \ \fbox {　 （２） 　} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {b}}= \ \fbox {　 （３） 　} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {c}}= \ \fbox {　 （４） 　} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {n}}= \ \fbox {　 （５） 　} \ \mathrm {[A]} \ \)となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.650-\mathrm {j}0.342　　　　　&（ロ）&　0.406-\mathrm {j}0.214　　　　　&（ハ）&　9.35+\mathrm {j}0.342 \\[ 5pt ] &（ニ）&　11.9-\mathrm {j}6.26　　　　　&（ホ）&　-4.00-\mathrm {j}6.93　　　　　&（ヘ）&　0.575-\mathrm {j}0.303 \\[ 5pt ] &（ト）&　6.50-\mathrm {j}3.42　　　　　&（チ）&　2.37-\mathrm {j}1.25　　　　　&（リ）&　10.0+\mathrm {j}0.00 \\[ 5pt ] &（ヌ）&　0.520-\mathrm {j}0.274　　　　　&（ル）&　-3.13+\mathrm {j}5.41　　　　　&（ヲ）&　1.30-\mathrm {j}0.685 \\[ 5pt ] &（ワ）&　2.88-\mathrm {j}1.52　　　　　&（カ）&　-3.53+\mathrm {j}5.63　　　　　&（ヨ）&　-4.52-\mathrm {j}6.65 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

不平衡負荷を接続した三相交流回路の回路計算に関する問題です。
電気回路の基本的な公式以外は使用しない問題ですが，計算量が多く，選択肢が絞れないため，多くの受験生を悩ませた問題と言えます。
ミルマンの定理やベクトルオペレータを使用すれば幾分計算量は減るかと思いますので，参考にしてみてください。

1.ミルマンの定理
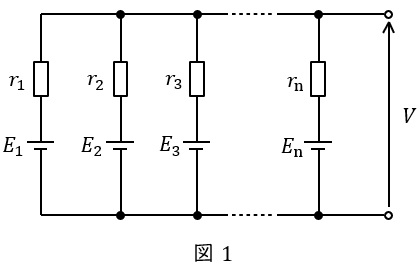
図1のような，電源\( \ E_{1}，E_{2}，\cdots ，E_{\mathrm {n}} \ \)と抵抗\( \ r_{1}，r_{2}，\cdots ，r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は，
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。電源がない時は\( \ E=0 \ \)を代入すれば，ミルマンの定理は成立します。

2.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は，\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり，
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ] &=& 1 \\[ 5pt ] \end{eqnarray}
\] となります。上記より，
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ] 1+a+a^{2}&=& 0 \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

【解答】

(1)解答：ト
負荷中性点の電圧\( \ {\dot V}_{\mathrm {n}} \ \)を求める式について，ミルマンの定理を適用すると，ワンポイント解説「1.ミルマンの定理」の通り，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {n}}&=&\frac {\displaystyle \frac {{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}}+\frac {{\dot E}_{\mathrm {b}}}{{\dot Z}_{\mathrm {b}}}+\frac {{\dot E}_{\mathrm {c}}}{{\dot Z}_{\mathrm {c}}}+\frac {0}{{\dot Z}_{\mathrm {n}}}}{\displaystyle \frac {1}{{\dot Z}_{\mathrm {a}}}+\frac {1}{{\dot Z}_{\mathrm {b}}}+\frac {1}{{\dot Z}_{\mathrm {c}}}+\frac {1}{{\dot Z}_{\mathrm {n}}}} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ {\dot E}_{\mathrm {a}}=100 \ \mathrm {[V]} \ \)，\( \ \displaystyle {\dot E}_{\mathrm {b}}=100a^{2} \ \mathrm {[V]} \ \)，\( \ \displaystyle {\dot E}_{\mathrm {c}}=100a \ \mathrm {[V]} \ \)であることを利用して各値を代入すると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {n}}&=&\frac {\displaystyle \frac {100}{10}+\frac {100a^{2}}{12.5}+\frac {100a}{16}+\frac {0}{5}}{\displaystyle \frac {1}{10}+\frac {1}{12.5}+\frac {1}{16}+\frac {1}{5}} \\[ 5pt ] &=&\frac {\displaystyle \frac {4000+3200a^{2}+2500a}{400}}{\displaystyle \frac {40+32+25+80}{400}} \\[ 5pt ] &=&\frac {4000+3200a^{2}+2500a}{177} \\[ 5pt ] &=&\frac {1500+700a^{2}+2500\left( 1+a^{2}+a\right) }{177} \\[ 5pt ] &=&\frac {1500+700a^{2}}{177}　 \left( ∵1+a^{2}+a=0\right) \\[ 5pt ] &=&\frac {1500+700\times \left( \displaystyle -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) }{177} \\[ 5pt ] &≒&6.50-\mathrm {j}3.42 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ハ
\( \ \mathrm {a} \ \)相について，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}}-{\dot Z}_{\mathrm {a}}{\dot I}_{\mathrm {a}}&=&{\dot V}_{\mathrm {n}} \\[ 5pt ] {\dot I}_{\mathrm {a}}&=&\frac {{\dot E}_{\mathrm {a}}-{\dot V}_{\mathrm {n}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}&=&\frac {100-\left( 6.50-\mathrm {j}3.42\right) }{10} \\[ 5pt ] &=&9.35+\mathrm {j}0.342 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
\( \ \mathrm {b} \ \)相について，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {b}}-{\dot Z}_{\mathrm {b}}{\dot I}_{\mathrm {b}}&=&{\dot V}_{\mathrm {n}} \\[ 5pt ] {\dot I}_{\mathrm {b}}&=&\frac {{\dot E}_{\mathrm {b}}-{\dot V}_{\mathrm {n}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}&=&\frac {100\times \left( \displaystyle -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) -\left( 6.50-\mathrm {j}3.42\right) }{12.5} \\[ 5pt ] &≒&-4.52-\mathrm {j}6.65 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
\( \ \mathrm {c} \ \)相について，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {c}}-{\dot Z}_{\mathrm {c}}{\dot I}_{\mathrm {c}}&=&{\dot V}_{\mathrm {n}} \\[ 5pt ] {\dot I}_{\mathrm {c}}&=&\frac {{\dot E}_{\mathrm {c}}-{\dot V}_{\mathrm {n}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}}&=&\frac {100\times \left( \displaystyle -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) -\left( 6.50-\mathrm {j}3.42\right) }{16} \\[ 5pt ] &≒&-3.53+\mathrm {j}5.63 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
中性線について，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {n}}{\dot I}_{\mathrm {n}}&=&{\dot V}_{\mathrm {n}} \\[ 5pt ] {\dot I}_{\mathrm {n}}&=&\frac {{\dot V}_{\mathrm {n}}}{{\dot Z}_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {n}}&=&\frac {6.50-\mathrm {j}3.42}{5} \\[ 5pt ] &=&1.30-\mathrm {j}0.684 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。