【問題】
【難易度】★★★★★(難しい)
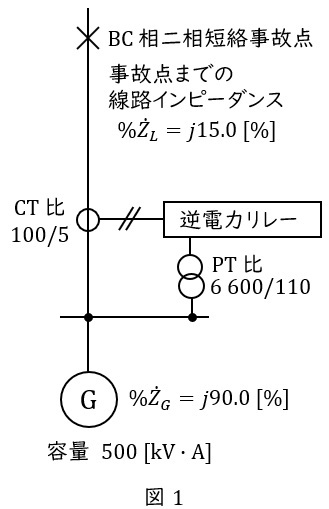
分散形電源を連系し,単独運転を検出するために逆電力リレーを設置した図1のような系統を考える。送電線に短絡事故が発生した場合の逆電カリレーの動作について,次の問に答えよ。
ただし,分散形電源は同期機であり,事故点よりも系統側のインピーダンス,負荷電流,短絡のアーク抵抗は無視するものとする。また,各インピーダンスは正相・逆相共に同じとし,\( \ 500 \ \mathrm {[kV\cdot A]} \ \),\( \ 6 \ 600 \ \mathrm {[V]} \ \)を基準容量,基準電圧とする。
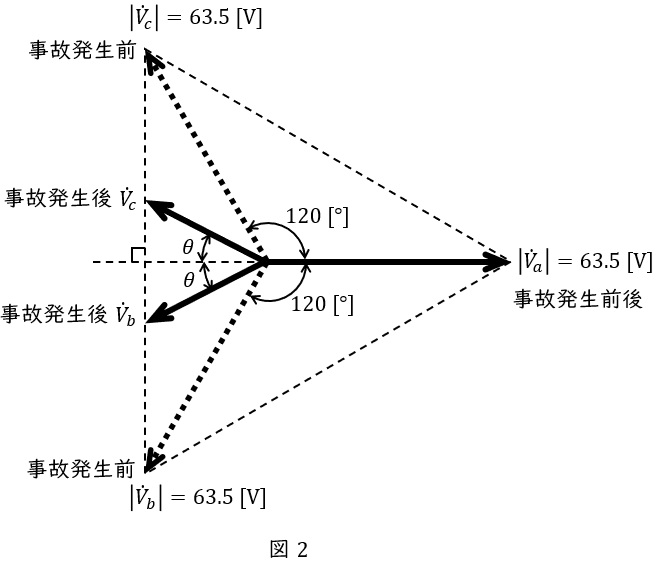
(1) 図1に示す地点で送電線に\( \ \mathrm {BC} \ \)相二相短絡事故が発生したとする。事故発生前及び発生後について,逆電カリレーの\( \ \mathrm {PT} \ \)が検出する\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)相間の電圧\( \ \left| {\dot V}_{bc}\right| \ \mathrm {[V]} \ \)(二次側換算値)を求めよ。ただし,二相短絡事故発生前後の\( \ \mathrm {PT} \ \)二次側電圧\( \ {\dot V}_{a} \ \),\( \ {\dot V}_{b} \ \),\( \ {\dot V}_{c} \ \)の関係は、図2のとおりとする。
(2) 上記の送電線事故発生時に流れる短絡事故電流の大きさを単位法で求めよ。
(3) 上記の送電線事故発生時に,逆電力リレーの\( \ \mathrm {PT} \ \),\( \ \mathrm {CT} \ \)が検出する\( \ \mathrm {B} \ \)相の電圧\( \ {\dot V}_{b} \ \mathrm {[V]} \ \)及び電流\( \ {\dot I}_{b} \ \mathrm {[A]} \ \)(いずれも二次側換算のベクトル値)を求めよ。なお,図2中の\( \ {\dot V}_{a} \ \)をベクトルの基準とする。
(4) 上記の送電線事故発生時に,逆電力リレーで検出される電力は,逆電力リレーの動作域にあるかどうか,根拠とともに示せ。ただし,逆電力リレーの動作検出は\( \ 3\cdot {\dot V}_{b} \cdot {\overline {\dot I}}_{b} \ \)で行われる仕様であるものとし,リレー動作域は,一次側換算で\( \ 50.0 \ \mathrm {[kW]} \ \)以上と設定されている。
【ワンポイント解説】
二相短絡事故が発生した場合の逆電カリレーの動作に関する問題です。
一種では比較的出題されやすい対称座標法を用いた問題ですが,計算量が非常に多く\( \ 30 \ \)分で解くことはかなり厳しい問題であるかと思います。
試験センター解答では単純にインピーダンスの按分と\( \ \displaystyle {\dot I}_{1}=\frac {{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \ \)を用いて解いているので,覚えている前提の出題かもしれません。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
2.対称座標法
故障計算をする際に非常に便利な方法で,以下のように定義し対称座標変換されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)事故発生前後の逆電カリレーの\( \ \mathrm {PT} \ \)が検出する電圧\( \ \left| {\dot V}_{bc}\right| \ \mathrm {[V]} \ \)(二次側換算値)
事故発生前,逆電カリレーの\( \ \mathrm {PT} \ \)が検出する電圧は図2より,
\[
\begin{eqnarray}
\left| {\dot V}_{bc}\right| &=&\sqrt {3}\left| {\dot V}_{b}\right| \\[ 5pt ]
&=&\sqrt {3}\times 63.5 \\[ 5pt ]
&≒&109.99 → 110 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,\( \ \mathrm {BC} \ \)相二相短絡事故が発生すると,事故点での電圧を\( \ {\dot V}_{a}^{\prime } \ \),\( \ {\dot V}_{b}^{\prime } \ \),\( \ {\dot V}_{c}^{\prime } \ \)とすれば,\( \ {\dot V}_{b}^{\prime }={\dot V}_{c}^{\prime } \ \),\( \ {\dot I}_{a}=0 \ \),\( \ {\dot I}_{b}=-{\dot I}_{c} \ \)が成立するので,零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \),零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)として関係式を立てると,ワンポイント解説「2.対称座標法」の通り,
\[
\begin{eqnarray}
{\dot V}_{a}^{\prime } &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} &・・・・・・・・・・・・ ①& \\[ 5pt ]
{\dot V}_{b}^{\prime } &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2}={\dot V}_{c}^{\prime } &・・・・・・・・・・・・ ②& \\[ 5pt ]
{\dot V}_{c}^{\prime } &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}={\dot V}_{b}^{\prime } &・・・・・・・・・・・・ ③& \\[ 5pt ]
{\dot I}_{a} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2}=0 &・・・・・・・・・・・・ ④& \\[ 5pt ]
{\dot I}_{b} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}=-{\dot I}_{c} &・・・・・・・・・・・・ ⑤& \\[ 5pt ]
{\dot I}_{c} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}=-{\dot I}_{b} &・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。②及び③より,
\[
\begin{eqnarray}
{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
a^{2}{\dot V}_{1} + a{\dot V}_{2} &=&a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\left( a^{2}-a\right) {\dot V}_{1}&=&\left( a^{2}-a\right) {\dot V}_{2} \\[ 5pt ]
{\dot V}_{1}&=&{\dot V}_{2} \ \ \ &・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となり,⑤及び⑥より,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &=&-\left( {\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}\right) \\[ 5pt ]
2{\dot I}_{0}+ \left( a^{2}+a\right) {\dot I}_{1} + \left( a+a^{2}\right) {\dot I}_{2} &=&0 \\[ 5pt ]
2{\dot I}_{0}- {\dot I}_{1} -{\dot I}_{2} &=&0 \left( ∵a+a^{2}+1=0\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。さら④を上式に加えれば,
\[
\begin{eqnarray}
3{\dot I}_{0} &=&0 \\[ 5pt ]
{\dot I}_{0} &=&0 &・・・・・・・・・・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となり,これを④に代入すれば,
\[
\begin{eqnarray}
{\dot I}_{1} + {\dot I}_{2} &=&0 \\[ 5pt ]
{\dot I}_{1} &=&-{\dot I}_{2} \ \ \ \ &・・・・・・・・・・・・・・・・・・ ⑨& \\[ 5pt ]
\end{eqnarray}
\]
となる。⑦~⑨を発電機の基本式に適用すると,正相・逆相インピーダンスが等しいことに注意すれば,
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
&=&-{\dot Z}_{0}\times 0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{a}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
&=&{\dot E}_{a}-\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2} {\dot I}_{2} \\[ 5pt ]
&=&\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ {\dot V}_{1}={\dot V}_{2} \ \)より,
\[
\begin{eqnarray}
{\dot E}_{a}-\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} &=&\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} \\[ 5pt ]
2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} &=&{\dot E}_{a} \\[ 5pt ]
{\dot I}_{1}&=&\frac {{\dot E}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,\( \ {\dot V}_{1}={\dot V}_{2} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{1}={\dot V}_{2} &=&{\dot E}_{a}-\left( {\dot Z}_{L}+{\dot Z}_{G}\right) {\dot I}_{1} \\[ 5pt ]
&=&{\dot E}_{a}-\left( {\dot Z}_{L}+{\dot Z}_{G}\right) \cdot \frac {{\dot E}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
&=&\frac {{\dot E}_{a}}{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ {\dot V}_{a}^{\prime } \ \),\( \ {\dot V}_{b}^{\prime }={\dot V}_{c}^{\prime } \ \)及び\( \ {\dot I}_{b}=-{\dot I}_{c} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{a}^{\prime } &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
&=& 2{\dot V}_{1} \\[ 5pt ]
&=& {\dot E}_{a} \\[ 5pt ]
{\dot V}_{b}^{\prime }={\dot V}_{c}^{\prime } &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
&=&0+ a^{2}{\dot V}_{1} + a{\dot V}_{1} \\[ 5pt ]
&=&\left( a^{2}+a \right) {\dot V}_{1} \\[ 5pt ]
&=&- {\dot V}_{1} \\[ 5pt ]
&=&-\frac {{\dot E}_{a}}{2} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}^{\prime }}{2} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2} \left( {\dot I}_{a}=0 \ なので \ {\dot V}_{a}={\dot V}_{a}^{\prime } \right) \\[ 5pt ]
{\dot I}_{b}=-{\dot I}_{c} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
&=&0+ a^{2}{\dot I}_{1} – a{\dot I}_{1} \\[ 5pt ]
&=&\left( a^{2}-a \right) {\dot I}_{1} \\[ 5pt ]
&=&\left( \frac {-1-j\sqrt {3}}{2}- \frac {-1+j\sqrt {3}}{2} \right) {\dot I}_{1} \\[ 5pt ]
&=&-j\sqrt {3} {\dot I}_{1} \\[ 5pt ]
&=&-j\frac {\sqrt {3}{\dot E}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
&=&-j\frac {\sqrt {3}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } ・・・・・・・・・・ ⑩ \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,逆電カリレーの\( \ \mathrm {PT} \ \)が検出する電圧\( \ {\dot V}_{b} \ \)及び\( \ {\dot V}_{c} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{b} &=&{\dot V}_{b}^{\prime }+{\dot Z}_{L}{\dot I}_{b} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2}+{\dot Z}_{L}\left\{ -j\frac {\sqrt {3}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) }\right\} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2}-j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \ ・・・・・・・・・・ ⑪ \\[ 5pt ]
{\dot V}_{c} &=&{\dot V}_{c}^{\prime }+{\dot Z}_{L}{\dot I}_{c} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2}+{\dot Z}_{L}\cdot j\frac {\sqrt {3}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2}+j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,事故発生後,逆電カリレーの\( \ \mathrm {PT} \ \)が検出する電圧は,
\[
\begin{eqnarray}
{\dot V}_{bc} &=& {\dot V}_{b}-{\dot V}_{c} \\[ 5pt ]
&=&-\frac {{\dot V}_{a}}{2}-j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) }-\left\{ -\frac {{\dot V}_{a}}{2}+j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) }\right\} \\[ 5pt ]
&=&-j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{{\dot Z}_{L}+{\dot Z}_{G}} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさは,
\[
\begin{eqnarray}
\left| {\dot V}_{bc}\right| &=&\left| -j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{ {\dot Z}_{L}+{\dot Z}_{G} }\right| \\[ 5pt ]
&=&\left| -j\frac {\sqrt {3}{\dot Z}_{L}}{{\dot Z}_{L}+{\dot Z}_{G}}{\dot V}_{a}\right| \\[ 5pt ]
&=&\frac {\sqrt {3}\times 0.15}{0.15+0.90}\times 63.5 \\[ 5pt ]
&≒&15.712 → 15.7 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※試験センター解答においては最後の式のみを用い,按分されると説明されています。
(2)送電線事故発生時に流れる短絡事故電流の大きさを単位法で求める
⑩より,送電線事故発生時に流れる短絡事故電流の大きさ\( \ \left| {\dot I}_{b}\right| \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\left| {\dot I}_{b}\right| &=&\left| -j\frac {\sqrt {3}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) }\right| \\[ 5pt ]
&=&\frac {\sqrt {3}\times 1.0}{2\times \left( 0.15+0.90\right) } \\[ 5pt ]
&≒&0.824 \ 79 → 0.825 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)送電線事故発生時に,逆電力リレーの\( \ \mathrm {PT} \ \),\( \ \mathrm {CT} \ \)が検出する\( \ \mathrm {B} \ \)相の電圧\( \ {\dot V}_{b} \ \mathrm {[V]} \ \)及び電流\( \ {\dot I}_{b} \ \mathrm {[A]} \ \)
⑪より,\( \ {\dot V}_{b} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{b} &=&-\frac {{\dot V}_{a}}{2}-j\frac {\sqrt {3}{\dot Z}_{L}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
&=&-\frac {1.0}{2}-j\frac {\sqrt {3}\times j0.15\times 1.0}{2\times \left( j0.15+j0.90\right) } \\[ 5pt ]
&≒&-0.5-j0.123 \ 72 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
なので,\( \ {\dot V}_{b} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{b} &=&\left( -0.5-j0.123 \ 72\right) \times 63.5 \\[ 5pt ]
&≒&-31.75-j7.856 \ 2 → -31.8-j7.86 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,⑩より\( \ {\dot I}_{b} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{b}&=&-j\frac {\sqrt {3}{\dot V}_{a}}{2\left( {\dot Z}_{L}+{\dot Z}_{G}\right) } \\[ 5pt ]
&=&-j\frac {\sqrt {3}\times 1.0}{2\times \left( j0.15+j0.90\right) } \\[ 5pt ]
&≒&-0.824 \ 79 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,基準容量\( \ P_{n}=500 \ \mathrm {[kV\cdot A]} \ \),基準電圧\( \ V_{n}=6 \ 600 \ \mathrm {[V]} \ \)より,基準電流\( \ I_{n} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{n} &=&\frac {P_{n}}{\sqrt {3}V_{n}} \\[ 5pt ]
&=&\frac {500 \times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ]
&≒&43.739 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,\( \ {\dot I}_{b} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{b}&=&-0.824 \ 79\times 43.739 \times \frac {5}{100} \\[ 5pt ]
&≒&-1.803 \ 8 → -1.80 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)逆電力リレーで検出される電力は,逆電力リレーの動作域にあるかどうか
題意より,逆電力リレーで検出される電力は,
\[
\begin{eqnarray}
3\cdot {\dot V}_{b} \cdot {\overline {\dot I}}_{b}&=&3\times \left( -31.75-j7.8562 \right) \times \left( -1.803 \ 8 \right) \\[ 5pt ]
&≒&171.82+j 42.513 \\[ 5pt ]
\end{eqnarray}
\]
となり,有効電力を一次側換算した値\( \ P \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P&=&171.82\times \frac {6 \ 600}{110}\times \frac {100}{5} \\[ 5pt ]
&≒&206 \ 184 \ \mathrm {[W]} → 206 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,リレー動作域である\( \ 50.0 \ \mathrm {[kW]} \ \)以上である。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん