《理論》〈電気回路〉[H19:問5]単相の需要家を接続した三相交流回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を記述用紙の解答欄に記入しなさい。ただし，答の有効数字は$ \ 3 \ $けたとし，整数となる場合は整数で解答してもよい。

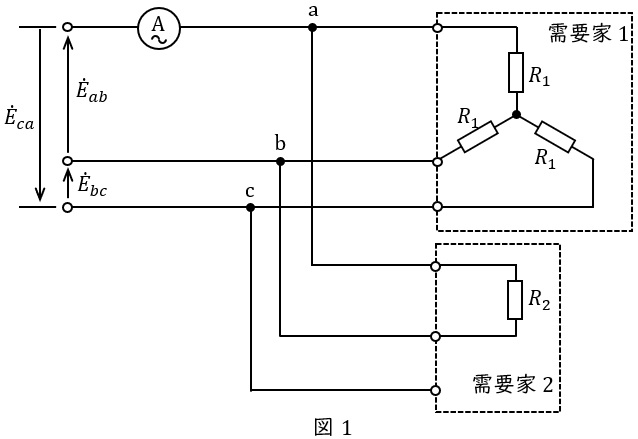
対称三相電源$ \ {\dot E}_{ab} = 200∠0^{\circ } \ \mathrm {[V]} \ $，$ \ {\dot E}_{bc} = 200∠{-120}^{\circ } \ \mathrm {[V]} \ $，$ \ {\dot E}_{ca} = 200∠{-240}^{\circ } \ \mathrm {[V]} \ $が，図1のように需要家$ \ 1 \ $と需要家$ \ 2 \ $に接続されている。需要家$ \ 1 \ $では，一相当たり$ \ R_{1} = 20 \ \mathrm {[\Omega ]} \ $の$ \ \mathrm {Y} \ $形接続の抵抗負荷を使用している。また，需要家$ \ 2 \ $では，端子$ \ \mathrm {a-b} \ $間にのみ抵抗負荷$ \ R_{2} = 40 \ \mathrm {[\Omega ]} \ $を接続して使用している。このとき，需要家$ \ 1 \ $の三相消費電力は$ \ \fbox {　（１）　} \ \mathrm {[kW]} \ $であり，需要家$ \ 2 \ $の消費電力は$ \ \fbox {　（２）　} \ \mathrm {[kW]} \ $である。

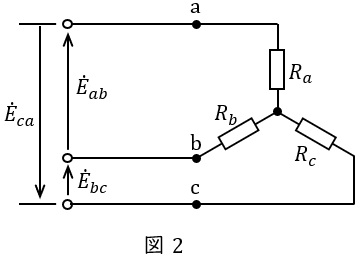
次に，図1における需要家$ \ 1 \ $と需要家$ \ 2 \ $の負荷回路を総合した合成等価回路として，図2の$ \ \mathrm {Y} \ $形三相回路を作成した。この等価回路で考えれば，需要家$ \ 1 \ $と需要家$ \ 2 \ $の総合電力は，$ \ 3 \ $個の抵抗で消費される総合電力に等しいことになる。この等価回路において，$ \ \mathrm {c} \ $相の等価抵抗$ \ R_{c} \ $は$ \ \fbox {　（３）　} \ \mathrm {[\Omega ]} \ $となり，この抵抗が分担する消費電力は$ \ \fbox {　（４）　} \ \mathrm {[kW]} \ $である。

また，$ \ \mathrm {a} \ $相の電流計の指示値は$ \ \fbox {　（５）　} \ \mathrm {[A]} \ $である。

【ワンポイント解説】

単相の需要家を接続した三相交流回路に関する問題です。
電源からみると不平衡負荷となる交流回路ですが，(3)と(4)以外の選択肢は$ \ 2 \ $種までで学習した内容で十分に対応できます。不平衡負荷の$ \ \Delta -\mathrm {Y} \ $変換は$ \ 1 \ $種では必須の知識となりますので，しっかりと変換できるようにしておきましょう。

1.$ \ \Delta -\mathrm {Y} \ $変換と$ \ \mathrm {Y}-\Delta \ $変換
①$ \ \Delta -\mathrm {Y} \ $変換
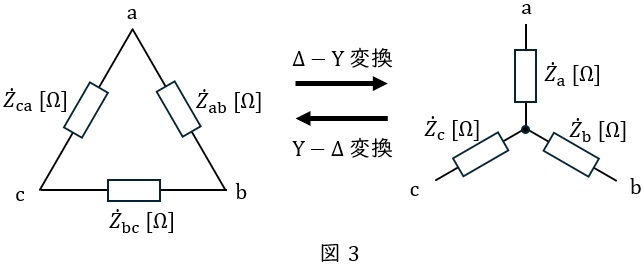
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②$ \ \mathrm {Y}-\Delta \ $変換
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.$ \ \mathrm {Y} \ $結線における相電圧と線間電圧の関係
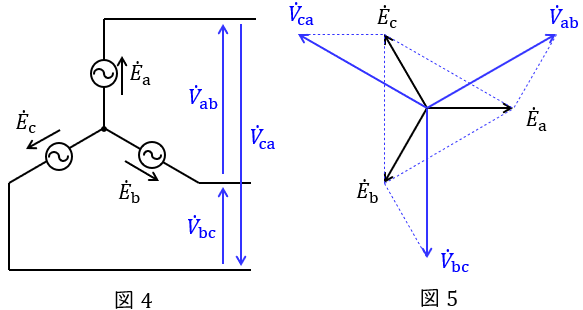
図4のような三相対称電源がある時，線間電圧と相電圧の関係は図5のベクトル図のようになり，線間電圧の大きさ$ \ V \ $は相電圧の大きさ$ \ E \ $と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ$ \ \displaystyle \frac {\pi }{6} $（30°)進みであることが分かります。

【解答】

(1)解答：$ \ 2 \ $
$ \ \mathrm {a} \ $相の相電圧$ \ {\dot E}_{a} \ \mathrm {[V]} \ $は，ワンポイント解説「2.$ \ \mathrm {Y} \ $結線における相電圧と線間電圧の関係」の通り，
\[
\begin{eqnarray}
{\dot E}_{a} &=&\frac {\left| {\dot E}_{ab}\right| }{\sqrt {3}}∠{\left( 0-30\right) }^{\circ } \ \mathrm {[V]} \\[ 5pt ] &=&\frac {200}{\sqrt {3}}∠{-30}^{\circ } \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，これが$ \ \mathrm {a} \ $相の$ \ R_{1} = 20 \ \mathrm {[\Omega ]} \ $に加わるから，このとき，需要家$ \ 1 \ $の三相消費電力$ \ P_{1} \ \mathrm {[kW]} \ $は，
\[
\begin{eqnarray}
P_{1} &=&3\cdot \frac {\left| {\dot E}_{a}\right| ^{2}}{R_{1}} \\[ 5pt ] &=&3\times \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{20} \\[ 5pt ] &=&2 \ 000 \ \mathrm {[W]}　→　2 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：$ \ 1 \ $
需要家$ \ 2 \ $の抵抗$ \ R_{2} = 40 \ \mathrm {[\Omega ]} \ $に加わる電圧は$ \ {\dot E}_{ab} = 200∠0^{\circ } \ \mathrm {[V]} \ $なので，需要家$ \ 2 \ $の消費電力$ \ P_{2} \ \mathrm {[kW]} \ $は，
\[
\begin{eqnarray}
P_{2} &=& \frac {\left| {\dot E}_{ab}\right| ^{2}}{R_{2}} \\[ 5pt ] &=& \frac {200^{2}}{40} \\[ 5pt ] &=&1 \ 000 \ \mathrm {[W]}　→　1 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：$ \ 25 \ $
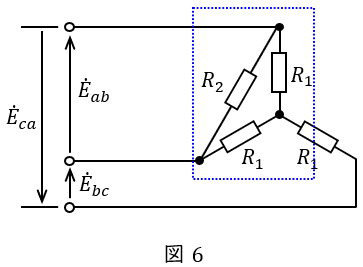
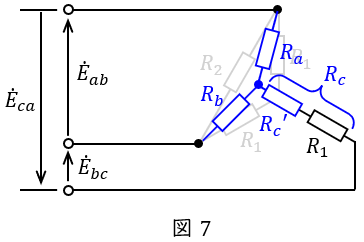
図1を書き換えると図6のようになり，図6の四角で囲った$ \ R_{1} \ $，$ \ R_{1} \ $，$ \ R_{2} \ $を$ \ \Delta -\mathrm {Y} \ $変換した回路が図7となる。図7の$ \ R_{a} \ \mathrm {[\Omega ]} \ $，$ \ R_{b} \ \mathrm {[\Omega ]} \ $，$ \ {R_{c}}^{\prime } \ \mathrm {[\Omega ]} \ $は，ワンポイント解説「1.$ \ \Delta -\mathrm {Y} \ $変換と$ \ \mathrm {Y}-\Delta \ $変換」の通り，
\[
\begin{eqnarray}
R_{a}&=&\frac {R_{2}R_{1}}{R_{1}+R_{1}+R_{2}} \\[ 5pt ] &=&\frac {40\times 20}{20+20+40} \\[ 5pt ] &=&10 \ \mathrm {[\Omega ]} \\[ 5pt ] R_{b}&=&\frac {R_{1}R_{2}}{R_{1}+R_{1}+R_{2}} \\[ 5pt ] &=&\frac {20\times 40}{20+20+40} \\[ 5pt ] &=&10 \ \mathrm {[\Omega ]} \\[ 5pt ] {R_{c}}^{\prime }&=&\frac {R_{1}R_{1}}{R_{1}+R_{1}+R_{2}} \\[ 5pt ] &=&\frac {20\times 20}{20+20+40} \\[ 5pt ] &=&5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ R_{c} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R_{c}&=&{R_{c}}^{\prime }+R_{1} \\[ 5pt ] &=&5+20 \\[ 5pt ] &=&25 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：$ \ 0.833 \ $
図1と図2を比較すると，$ \ \mathrm {c} \ $相に流れる電流は等しくなければならないから，図1より$ \ \mathrm {c} \ $相に流れる電流$ \ I_{c} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{c}&=&\frac {\left| {\dot E}_{c}\right| }{R_{1}} \\[ 5pt ] &=&\frac {\displaystyle \frac {200}{\sqrt {3}} }{20} \\[ 5pt ] &≒&5.773 \ 5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ R_{c} \ $が分担する消費電力$ \ P_{c} \ \mathrm {[kW]} \ $は，
\[
\begin{eqnarray}
P_{c}&=&R_{c}{I_{c}}^{2} \\[ 5pt ] &=&25\times 5.773 \ 5^{2} \\[ 5pt ] &≒&833.33 \ \mathrm {[W]}　→　0.833 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：$ \ 10.4 \ $
図1において，需要家$ \ 1 \ $の$ \ \mathrm {a} \ $相の抵抗$ \ R_{1} \ $に流れる電流$ \ {\dot I}_{a1} \ \mathrm {[A]} \ $及び需要家$ \ 2 \ $の抵抗$ \ R_{2} \ $に流れる電流$ \ {\dot I}_{a2} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{a1}&=&\frac {{\dot E}_{a}}{R_{1}} \\[ 5pt ] &=&\frac {\displaystyle \frac {200}{\sqrt {3}}∠{-30}^{\circ }}{20} \\[ 5pt ] &=&\frac {10}{\sqrt {3}}∠{-30}^{\circ } \\[ 5pt ] &=&\frac {10}{\sqrt {3}}\left\{ \cos \left( -30^{\circ }\right) +j\sin \left( -30^{\circ }\right) \right\} \\[ 5pt ] &=&\frac {10}{\sqrt {3}}\left( \frac {\sqrt {3}}{2} -j\frac {1}{2}\right) \\[ 5pt ] &≒&5-j2.886 \ 8 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{a2}&=&\frac {{\dot E}_{ab}}{R_{2}} \\[ 5pt ] &=&\frac {200∠0^{\circ }}{40} \\[ 5pt ] &=&5∠0^{\circ } \\[ 5pt ] &=&5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ \mathrm {a} \ $相の電流計に流れる電流$ \ {\dot I}_{a} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{a}&=&{\dot I}_{a1}+{\dot I}_{a2} \\[ 5pt ] &=&5-j2.886 \ 8+5 \\[ 5pt ] &=&10-j2.886 \ 8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，その大きさ$ \ \left| {\dot I}_{a}\right| \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
\left| {\dot I}_{a}\right| &=&\sqrt {10^{2}+{2.886 \ 8}^{2}} \\[ 5pt ] &≒&10.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。