《理論》〈電子理論〉[H28:問7] 演算増幅器を用いた回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

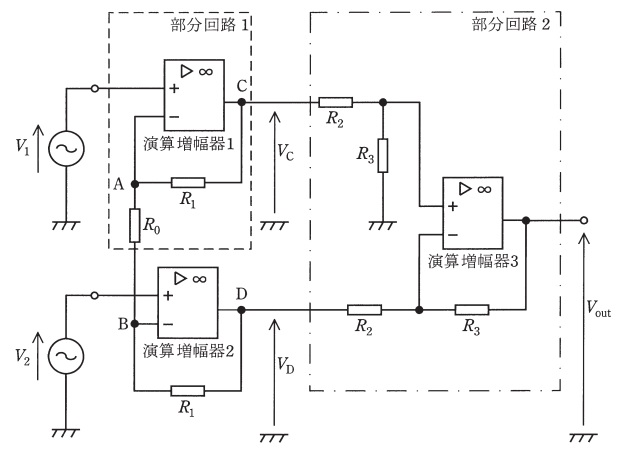
次の文章は，演算増幅器を用いた回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，演算増幅器の電圧増幅度(差動利得)と入力インピーダンスはそれぞれ無限大であり，出力インピーダンスは零であるとする。

まず，入力電圧として$ \ V_{1} \ $のみが存在し，$ \ V_{2} \ $が零のときを考える。このとき，$ \ \mathrm {B} \ $点の電位は$ \ \fbox {　（１）　} \ $となる。これより破線で囲まれた部分回路1は，$ \ V_{1} \ $を入力とした非反転増幅回路として動作することが分かる。このときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}}^{\prime } \ $は$ \ \fbox {　（２）　} \ \times V_{1} \ $となる。また，$ \ \mathrm {A} \ $点の電位は$ \ V_{1} \ $であり，$ \ V_{2} \ $は零であるため，演算増幅器2は$ \ \mathrm {A} \ $点を入力端子とした反転増幅回路として動作する。つまり，$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}}^{\prime } \ $は，$ \ \fbox {　（３）　} \ \times V_{1} \ $となる。
次に，入力電圧として$ \ V_{2} \ $のみが存在し，$ \ V_{1} \ $が零であるときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}}^{\prime \prime } \ $と$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}}^{\prime \prime } \ $を求める。$ \ V_{\mathrm {C}}^{\prime \prime } \ $と$ \ V_{\mathrm {D}}^{\prime \prime } \ $は先の結果と回路の対称性を考慮すると求められる。
最後に，$ \ V_{1} \ $と$ \ V_{2} \ $の両方が存在するときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}} \ $と$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}} \ $は，重ねの理を用いることでそれぞれ$ \ \fbox {　（４）　} \ $と求まる。
一点鎖線で囲まれた部分回路2は$ \ V_{\mathrm {C}} \ $と$ \ V_{\mathrm {D}} \ $を入力とする減算回路であり，出力電圧$ \ V_{\mathrm {out}} \ $は$ \ \displaystyle V_{\mathrm {out}}=\frac {R_{3}}{R_{2}}\times \left( V_{\mathrm {C}}-V_{\mathrm {D}}\right) \ $である。
以上の結果から図の回路は，出力電圧$ \ V_{\mathrm {out}} \ $が$ \ \fbox {　（５）　} \ \times \left( V_{1}-V_{2}\right) \ $で表される差動増幅回路であることが分かる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　-\frac {R_{3}}{R_{2}}\left( \frac {R_{0}+R_{1}}{R_{0}}\right) 　　　　　&（ロ）&　V_{\mathrm {C}}^{\prime }-V_{\mathrm {C}}^{\prime \prime }とV_{\mathrm {D}}^{\prime }-V_{\mathrm {D}}^{\prime \prime }　　　　&（ハ）&　\frac {R_{3}}{R_{2}}\left( \frac {R_{0}+2R_{1}}{R_{0}}\right) 　 \\[ 5pt ] &（ニ）&　-\frac {R_{2}}{R_{3}}\left( \frac {R_{0}+2R_{1}}{R_{0}}\right)　　　　　&（ホ）&　-V_{1}　　　　　&（ヘ）&　0 \\[ 5pt ] &（ト）&　V_{1}　　　　　&（チ）&　\frac {R_{1}}{R_{0}}　　　　　&（リ）&　-\frac {R_{1}R_{3}}{R_{0}R_{2}} \\[ 5pt ] &（ヌ）&　V_{\mathrm {C}}^{\prime }+V_{\mathrm {C}}^{\prime \prime }とV_{\mathrm {D}}^{\prime }+V_{\mathrm {D}}^{\prime \prime }　　　　　&（ル）&　-\frac {R_{1}}{R_{0}}　　　　　&（ヲ）&　V_{\mathrm {C}}^{\prime }+V_{\mathrm {D}}^{\prime }とV_{\mathrm {C}}^{\prime \prime }+V_{\mathrm {D}}^{\prime \prime } \\[ 5pt ] &（ワ）&　\frac {R_{0}+R_{1}}{R_{0}}　　　　　&（カ）&　\frac {R_{0}+2R_{1}}{R_{0}}　　　　　&（ヨ）&　-\frac {R_{0}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

問6の分布定数回路と比べると計算量が少ないため，電験一種受験者であれば比較的容易に解けたのではないでしょうか。二種と三種の復習となりますが，オペアンプの特徴に関してはよく理解しておくようにしましょう。

1.理想的なオペアンプの特徴
１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$ \ 0 \ \mathrm {V} \ $(バーチャルショート)となります。
２．入力インピーダンスが無限大です。したがって入力端子に電流は流れません。
３．出力インピーダンスがゼロです。

【解答】

(1)解答：ヘ
$ \ V_{2} \ $が零であり，ワンポイント解説「1.理想的なオペアンプの特徴」の通り，入力端子間の電圧は$ \ 0 \ \mathrm {V} \ $(バーチャルショート)となるので，$ \ \mathrm {B} \ $点の電位は$ \ 0 \ \mathrm {V} \ $となります。

(2)解答：ワ
(1)と同様に$ \ \mathrm {A} \ $点の電位は$ \ V_{1} \ $であるから，部分回路1内$ \ R_{0} \ $を流れる電流$ \ I_{\mathrm {R0}} \ $は，
\[
I_{\mathrm {R0}}=\frac {V_{1}}{R_{0}}
\] となる。また，ワンポイント解説「1.理想的なオペアンプの特徴」の通り，オペアンプ入力端子に電流は流れないので，電流$ \ I_{\mathrm {R0}} \ $はすべて部分回路1の$ \ R_{1} \ $側へ流れる。
よって，このときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}}^{\prime } \ $は，
\[
\begin{eqnarray}
V_{\mathrm {C}}^{\prime } &=& V_{1}+R_{1}I_{\mathrm {R0}} \\[ 5pt ] &=& V_{1}+R_{1}\frac {V_{1}}{R_{0}} \\[ 5pt ] &=&\frac {R_{0}+R_{1}}{R_{0}}V_{1}
\end{eqnarray}
\] と求められる。

(3)解答：ル
部分回路1内$ \ R_{0} \ $を流れる電流$ \ I_{\mathrm {R0}} \ $は，$ \ \mathrm {B} \ $点の後，演算増幅器2には電流が流れないので，すべて演算増幅器2の下の$ \ R_{1} \ $側へ流れる。よって，$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}}^{\prime } \ $は，
\[
\begin{eqnarray}
V_{\mathrm {D}}^{\prime } &=& 0-R_{1}I_{\mathrm {R0}} \\[ 5pt ] &=& 0-R_{1}\frac {V_{1}}{R_{0}} \\[ 5pt ] &=&-\frac {R_{1}}{R_{0}}V_{1}
\end{eqnarray}
\] と求められる。

(4)解答：ヌ
(2)，(3)と同様に入力電圧として$ \ V_{2} \ $のみが存在し，$ \ V_{1} \ $が零であるときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}}^{\prime \prime } \ $と$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}}^{\prime \prime } \ $は
\[
\begin{eqnarray}
V_{\mathrm {C}}^{\prime \prime } &=& -\frac {R_{1}}{R_{0}}V_{2} \\[ 5pt ] V_{\mathrm {D}}^{\prime \prime } &=& \frac {R_{0}+R_{1}}{R_{0}}V_{2}
\end{eqnarray}
\] と求められる。よって，$ \ V_{1} \ $と$ \ V_{2} \ $の両方が存在するときの$ \ \mathrm {C} \ $点の電位$ \ V_{\mathrm {C}} \ $と$ \ \mathrm {D} \ $点の電位$ \ V_{\mathrm {D}} \ $は，重ねの理を用いることで，
\[
\begin{eqnarray}
V_{\mathrm {C}} &=& V_{\mathrm {C}}^{\prime }+ V_{\mathrm {C}}^{\prime \prime } \\[ 5pt ] &=& \frac {R_{0}+R_{1}}{R_{0}}V_{1}-\frac {R_{1}}{R_{0}}V_{2} \\[ 5pt ] V_{\mathrm {D}} &=& V_{\mathrm {D}}^{\prime }+ V_{\mathrm {D}}^{\prime \prime } \\[ 5pt ] &=& -\frac {R_{1}}{R_{0}}V_{1}+ \frac {R_{0}+R_{1}}{R_{0}}V_{2}
\end{eqnarray}
\] と求められる。

(5)解答：ハ
題意より，出力電圧$ \ V_{\mathrm {out}} \ $は，$ \ \displaystyle V_{\mathrm {out}}=\frac {R_{3}}{R_{2}}\times \left( V_{\mathrm {C}}-V_{\mathrm {D}}\right) \ $で表されるから，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {R_{3}}{R_{2}}\times \left[ \frac {R_{0}+R_{1}}{R_{0}}V_{1}-\frac {R_{1}}{R_{0}}V_{2}-\left( -\frac {R_{1}}{R_{0}}V_{1}+ \frac {R_{0}+R_{1}}{R_{0}}V_{2}\right) \right] \\[ 5pt ] &=& \frac {R_{3}}{R_{2}}\times \left( \frac {R_{0}+2R_{1}}{R_{0}}V_{1}-\frac {R_{0}+2R_{1}}{R_{0}}V_{2}\right) \\[ 5pt ] &=& \frac {R_{3}}{R_{2}}\left( \frac {R_{0}+2R_{1}}{R_{0}}\right) \left( V_{1}-V_{2}\right)
\end{eqnarray}
\] と求められる。