【問題】
【難易度】★★★☆☆(普通)
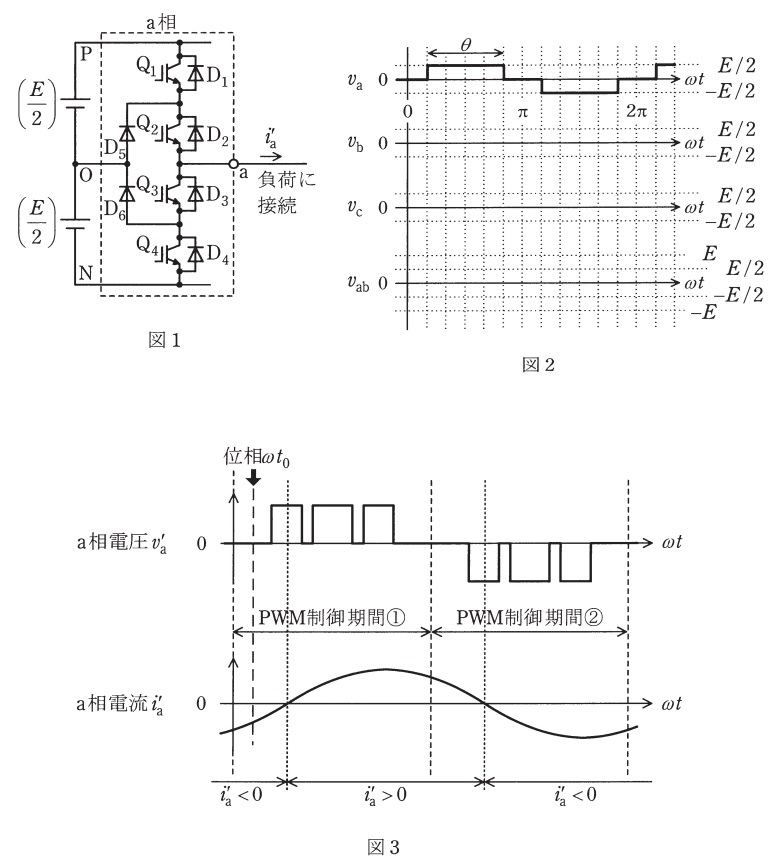
\( \ \mathrm {a} \ \)相→\( \ \mathrm {b} \ \)相→\( \ \mathrm {c} \ \)相の相順の三相\( \ 3 \ \)レベルインバータがあり,そのうち,図1には電圧\( \ E \ \)を\( \ 2 \ \)分割した直流電源とインバータの\( \ 1 \ \)相分である\( \ \mathrm {a} \ \)相の回路を示す。図2には\( \ 1 \ \)サイクルで正負\( \ 1 \ \)パルスの電圧を出力した場合の\( \ \mathrm {a} \ \)相電圧\( \ v_{\mathrm {a}} \ \)の波形を示す。また,図3には,\( \ \mathrm {PWM} \ \)制御を行って電圧を出力した場合の\( \ \mathrm {a} \ \)相電圧の\( \ v_{\mathrm {a}}^{\prime } \ \)と,図1に示す矢印を正の方向として正弦波とみなした場合の\( \ \mathrm {a} \ \)相電流\( \ i_{\mathrm {a}}^{\prime } \ \)の波形を示す。以下の問に答えよ。
(1) 図2の\( \ \mathrm {a} \ \)相電圧\( \ v_{\mathrm {a}} \ \)の波形を基準にして,他の\( \ \mathrm {b} \ \)相電圧\( \ v_{\mathrm {b}} \ \),\( \ \mathrm {c} \ \)相電圧\(v_{\mathrm {c}}\)及び\( \ \mathrm {b} \ \)相から\( \ \mathrm {a} \ \)相をみた線間電圧\( \ v_{\mathrm {ab}} \ \)のそれぞれの波形を,波形の大きさとスイッチングの位相が明確に分かるように,答案用紙に印刷されている図2に示せ。
(2) 図2の\( \ \mathrm {a} \ \)相電圧\( \ v_{\mathrm {a}} \ \)の波形のように,振幅が\( \ \displaystyle \frac {E}{2} \ \),正負のパルス幅が\( \ \theta \ \),角周波数が\( \ \omega \ \)の電圧波形は,次式のフーリエ級数展開ができる。
\[
\begin{eqnarray}
v&=&\frac {4}{\pi }\times \frac {E}{2}\displaystyle \sum_{ n = 1 }^{ \infty }\frac {(-1) ^{n-1}}{2n-1}\sin \frac { (2n-1) \theta }{2}\sin (2n-1) \omega t \\[ 5pt ]
\end{eqnarray}
\]
\( \ \displaystyle \theta =\frac {2\pi }{3}\mathrm{rad} \ \)のとき,線間電圧\( \ v_{\mathrm {ab}} \ \)波形に含まれる基本波の実効値\( \ V_{\mathrm {ab}} \ \)を\( \ E \ \)を用いて示せ。
(3) 図3に示す\( \ \mathrm {a} \ \)相電圧\( \ v_{\mathrm {a}}^{\prime } \ \)の\( \ \mathrm {PWM} \ \)制御期間①において,\( \ Q_{1}~Q_{4} \ \)のうち,オンしているデバイス,オフしているデバイス及び交互にスイッチングするデバイスはそれぞれどのデバイスであるかを答えよ。
(4) 図3に示す位相\( \ \omega t_{0} \ \)のときは,負荷から\( \ \mathrm {a} \ \)端子を通って,直流電源端子\( \ \mathrm {O} \ \)に向けて電流\( \ i_{\mathrm {a}}^{\prime } \ \)が流れている。この電流経路は「\( \ \mathrm {a} \ \)端子→デバイス\( \ \mathrm {A} \ \)→デバイス\( \ \mathrm {B} \ \)→\( \ \mathrm {O} \ \)端子」となるが,\( \ Q_{1}~Q_{4} \ \)及び\( \ D_{1}~D_{6} \ \)のうち,デバイス\( \ \mathrm {A} \ \)とデバイス\( \ \mathrm {B} \ \)はそれぞれどのデバイスであるかを答えよ。
(5) \( \ D_{5} \ \),\( \ D_{6} \ \)はクランプダイオードと呼ばれている。このダイオードの働きを説明せよ。
【ワンポイント解説】
(3)をじっくりと考えなければならないため,時間との勝負となりますが,ここをスムースに行けば,平成29年の問題で最も時間がかからない問題なので,機械制御では選択すべき問題と言えます。
【関連する「電気の神髄」記事】
さまざまな交流波形のフーリエ級数展開まとめ
三相電圧形3レベルインバータ
【解答】
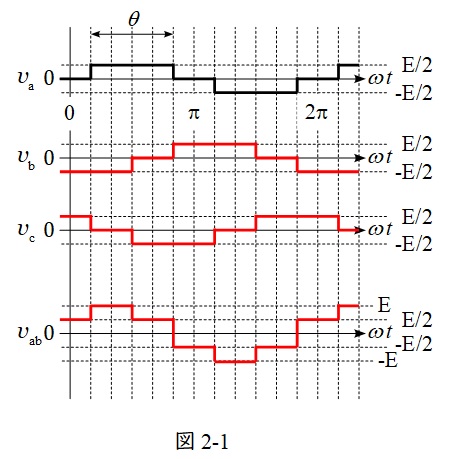
(1)\( \ \mathrm {b} \ \)相電圧\(v_{\mathrm {b}}\),\( \ \mathrm {c} \ \)相電圧\(v_{\mathrm {c}}\)及び\( \ \mathrm {b} \ \)相から\( \ \mathrm {a} \ \)相をみた線間電圧\( \ v_{\mathrm {ab}} \ \)のそれぞれの波形
\( \ \mathrm {a} \ \)相→\( \ \mathrm {b} \ \)相→\( \ \mathrm {c} \ \)相の順に\( \ 120° \ \)ずつ遅れるので,電圧波形は図2-1の通りとなる。
(2)基本波の実効値\( \ V_{\mathrm {ab}} \ \)
題意に沿って,\( \ \displaystyle \theta =\frac {2\pi }{3} \ \mathrm {rad} \ \),\( \ n=1 \ \)を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {a}}&=&\frac {4}{\pi }\times \frac {E}{2}\times \frac {(-1) ^{1-1}}{2\times 1-1}\sin \frac { (2\times 1-1) \times \frac {2\pi }{3} }{2}\sin (2\times 1-1) \omega t \\[ 5pt ]
&=&\frac {2E}{\pi }\times \sin \frac {\pi }{3}\sin \omega t \\[ 5pt ]
&=&\frac {\sqrt {3} E}{\pi }\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,線間電圧の実効値\( \ V_{\mathrm {ab}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {ab}}&=&\frac {\sqrt {3} \frac {\sqrt {3} E}{\pi }}{\sqrt {2}} \\[ 5pt ]
&=&\frac {3 E}{\sqrt {2}\pi} \\[ 5pt ]
&≒&0.67524E → 0.675E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {PWM} \ \)制御期間①において,\( \ Q_{1}~Q_{4} \ \)のうち,オンしているデバイス,オフしているデバイス及び交互にスイッチングするデバイス
\( \ \mathrm {PWM} \ \)制御期間①は電圧が\( \ \displaystyle \frac {E}{2} \ \)と\( \ 0 \ \)でスイッチングしており,かつ電流\( \ i_{\mathrm {a}}^{\prime } \ \)が正の場合と負の場合がある状況である。
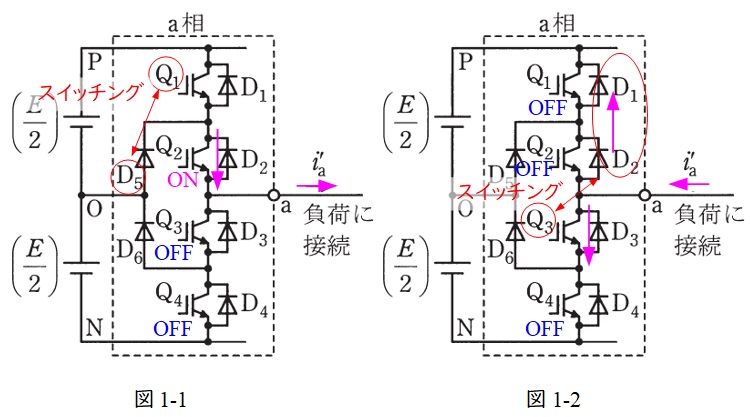
\( \ i_{\mathrm {a}}^{\prime } >0 \ \)の時は,図1-1の通り,電流の流れから,\( \ Q_{2} \ \)は常時\( \ \mathrm {ON} \ \),\( \ Q_{3} \ \),\( \ Q_{4} \ \)は常時\( \ \mathrm {OFF} \ \)となる。また,\( \ Q_{1} \ \)と\( \ D_{5} \ \)が交互にスイッチングする。
一方\( \ i_{a}^{\prime } <0 \ \)の時は,図1-2の通り,\( \ Q_{1} \ \),\( \ Q_{2} \ \),\( \ Q_{4} \ \)は常時\( \ \mathrm {OFF} \ \)となる。また,\( \ Q_{3} \ \)と\( \ D_{1} \ \),\( \ D_{2} \ \)が交互にスイッチングする。
(4)デバイス\( \ \mathrm {A} \ \)とデバイス\( \ \mathrm {B} \ \)はそれぞれどのデバイスであるか
図2の通り,\( \ \omega t_{0} \ \)のときは,\( \ i_{\mathrm {a}}^{\prime } < 0 \ \)で電圧が\( \ 0 \ \)である。よって,図1-2において,\( \ Q_{3} \ \)が\( \ \mathrm {ON} \ \)となるパターンである。よって電流経路は「\( \ \mathrm {a} \ \)端子→\( \ Q_{3} \ \)→\( \ D_{6} \ \)→\( \ \mathrm {O} \ \)端子」となる。
(5)クランプダイオードの働き
\( \ Q_{1}~Q_{4} \ \)が\( \ \mathrm {OFF} \ \)の時,それぞれのデバイスにかかる電圧が\( \ \displaystyle \frac {E}{2} \ \)になるような働きをしている。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん