《電力・管理》〈送電〉[H28:問3] 同期発電機に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

同期発電機の過励磁制限機能動作時の系統状態に関して，次の問に答えよ。

一機無限大母線系統で，同期発電機端子と無限大母線間は\(x_{\mathrm {L}}\)のリアクタンスのみで表現されている。また，界磁電圧に相当する発電機内部電圧は，飽和や抵抗分を無視して発電機の内部リアクタンスのみによって，①式で与えられるものとする。このとき，次の問に答えよ。ただし，無効電力は遅れ側を正とし，各量の単位は単位法とする。また，電力動揺は発生しないものとする。
\[
{\dot E}_{\mathrm {f}}={\dot V}_{\mathrm {g}}+\mathrm {j}x_{\mathrm {g}}\dot I　・・・・・・・・・・・・・・・・・　①
\] ただし，
　　\({\dot E}_{\mathrm {f}}\)：発電機界磁電圧(内部電圧)，　　\({\dot V}_{\mathrm {g}}\)：発電機端子電圧
　　\(x_{\mathrm {g}}\)：発電機内部リアクタンス，　　　\(\dot I \ \)：発電機電機子電流

(1)　発電機端子電圧の大きさ\(V_{\mathrm {g}}\)，無限大母線電圧の大きさ\(V_{\mathrm {i}}\)，発電機有効電力\(P_{\mathrm {g}}\)と\(x_{\mathrm {L}}\)及び\(x_{\mathrm {g}}\)と用いて，発電機無効電力\(Q_{\mathrm {g}}\)と発電機界磁電圧の大きさ\(E_{\mathrm {f}}\)を表す式は以下のように表される。\(A～D\)，\(F\)を\(x_{\mathrm {g}}\)，\(x_{\mathrm {L}}\)，\(V_{\mathrm {g}}\)，\(V_{\mathrm {i}}\)，\(P_{\mathrm {g}}\)，\(Q_{\mathrm {g}}\)を用いて表せ。

ただし，これらの量は全てスカラー量である。また，\(\delta \)は\({\dot V}_{\mathrm {i}}\)を基準とした\({\dot V}_{\mathrm {g}}\)の相差角である。
\[
\begin{eqnarray}
Q_{\mathrm {g}}=\frac {A}{x_{\mathrm {L}}}\left( A-B\cos \delta \right)　・・・・・・・・・・・・・　② \\[ 5pt ] ただし， \cos \delta =\sqrt {1-\left( \frac {C}{AB}\right) ^{2}}　・・・・・・・・・　③ \\[ 5pt ] E_{\mathrm {f}}=\sqrt {\left( V_{\mathrm {g}} +D\right) ^{2} +F^{2}}　・・・・・・・・・・・・・　④
\end{eqnarray}
\]

(2)　\(x_{\mathrm {L}}=0.4\)，\(x_{\mathrm {g}}=1.8\)，\(V_{\mathrm {g}}=1.03\)，\(V_{\mathrm {i}}=0.83\)，\(P_{\mathrm {g}}=0.9\)のときの上記の\(Q_{\mathrm {g}}\)及び\(E_{\mathrm {f}}\)を求めよ。

(3)　界磁電圧が長時間大きくなったままでは，界磁巻線の過熱などが発生するので，\(\mathrm {OEL}\)(過励磁制限機能)が動作する。ある\(\mathrm {OEL}\)の方式では，\(\mathrm {OEL}\)動作時には界磁電圧が一定値に制限される。界磁電圧の大きさ\(E_{\mathrm {f}}\)が与えられた場合の，\(V_{\mathrm {g}}\)を表す式は以下のように表される。\(G\)，\(H\)，\(J\)を\(x_{\mathrm {g}}\)，\(x_{\mathrm {L}}\)，\(V_{\mathrm {i}}\)，\(P_{\mathrm {g}}\)，\(E_{\mathrm {f}}\)を用いて表せ。なお，\(\delta _{\mathrm {f}}\)は\({\dot V}_{\mathrm {i}}\)を基準とした\({\dot E}_{\mathrm {f}}\)の相差角である。
\[
\begin{eqnarray}
V_{\mathrm {g}}=\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}\sqrt {G+H\cos \delta _{\mathrm {f}}}　・・・・・・・・・・　⑤ \\[ 5pt ] ただし， \cos \delta _{\mathrm {f}}=\sqrt {1-J ^{2}}　・・・・・・・・・・・・　⑥
\end{eqnarray}
\]

【ワンポイント解説】

特別難しい公式は使用しませんが，途中の計算が面倒な問題です。本問の類題は過去にも出題されているため，無効電力や有効電力の導出やベクトル演算は早くできるようにしておきましょう。

1.オイラーの公式
極座標空間において，
\[
\mathrm {e}^{\mathrm {j}\theta }=\cos \theta +\mathrm {j}\sin \theta
\] となります。

【解答】

(1)\(A～D\)，\(F\)を\(x_{\mathrm {g}}\)，\(x_{\mathrm {L}}\)，\(V_{\mathrm {g}}\)，\(V_{\mathrm {i}}\)，\(P_{\mathrm {g}}\)，\(Q_{\mathrm {g}}\)を用いて表す
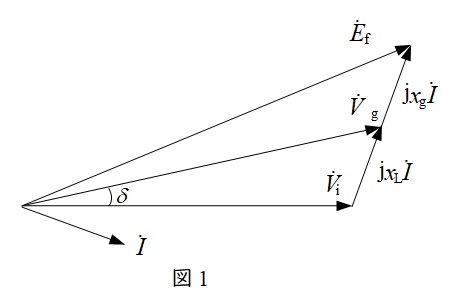
題意に沿ってベクトル図を描くと図1のようになる。これより，\({\dot V}_{\mathrm {i}}\)を基準にすると，\({\dot V}_{\mathrm {g}}=V_{\mathrm {g}}\mathrm {e}^{\mathrm {j}\delta }\)で表される。図1より，
\[
{\dot V}_{\mathrm {g}}={\dot V}_{\mathrm {i}}+\mathrm {j}x_{\mathrm {L}}\dot I
\] となるから\(\dot I\)について整理すると，
\[
\begin{eqnarray}
\dot I&=&\frac {{\dot V}_{\mathrm {g}}-{\dot V}_{\mathrm {i}}}{\mathrm {j}x_{\mathrm {L}}} \\[ 5pt ] &=&\frac {V_{\mathrm {g}}\mathrm {e}^{\mathrm {j}\delta }-V_{\mathrm {i}}}{\mathrm {j}x_{\mathrm {L}}}
\end{eqnarray}
\] となる。よって，発電機電力は遅れ無効電力を正とすると，
\[
\begin{eqnarray}
P_{\mathrm {g}}+\mathrm {j}Q_{\mathrm {g}}&=&{\dot V}_{\mathrm {g}}\overline {\dot I} \\[ 5pt ] &=&V_{\mathrm {g}}\mathrm {e}^{\mathrm {j}\delta }\frac {V_{\mathrm {g}}\mathrm {e}^{-\mathrm {j}\delta }-V_{\mathrm {i}}}{-\mathrm {j}x_{\mathrm {L}}} \\[ 5pt ] &=&\frac {V_{\mathrm {g}}^{2}-V_{\mathrm {g}}V_{\mathrm {i}}\mathrm {e}^{\mathrm {j}\delta }}{-\mathrm {j}x_{\mathrm {L}}} \\[ 5pt ] &=&\mathrm {j}\frac {V_{\mathrm {g}}^{2}}{x_{\mathrm {L}}}-\mathrm {j}\frac {V_{\mathrm {g}}V_{\mathrm {i}}}{x_{\mathrm {L}}}\left( \cos \delta +\mathrm {j}\sin \delta \right) \\[ 5pt ] &=&\frac {V_{\mathrm {g}}V_{\mathrm {i}}}{x_{\mathrm {L}}}\sin \delta +\mathrm {j}\frac {V_{\mathrm {g}}}{x_{\mathrm {L}}}\left( V_{\mathrm {g}}-V_{\mathrm {i}}\cos \delta \right)
\end{eqnarray}
\] と求められるので，②と上式を比較すると，\(A=V_{\mathrm {g}}\)，\(B=V_{\mathrm {i}}\)となる。また，\(\displaystyle P_{\mathrm {g}}=\frac {V_{\mathrm {g}}V_{\mathrm {i}}}{x_{\mathrm {L}}}\sin \delta\)より，
\[
\sin \delta=\frac {P_{\mathrm {g}}x_{\mathrm {L}}}{V_{\mathrm {g}}V_{\mathrm {i}}}
\] となるので，
\[
\begin{eqnarray}
\cos \delta&=&\sqrt {1-\sin ^{2}\delta } \\[ 5pt ] &=&\sqrt {1-\left( \frac {P_{\mathrm {g}}x_{\mathrm {L}}}{V_{\mathrm {g}}V_{\mathrm {i}}}\right) ^{2} }
\end{eqnarray}
\] と求められる。よって，③と上式を比較すると，\(C=P_{\mathrm {g}}x_{\mathrm {L}}\)となる。
次に，\({\dot V}_{\mathrm {g}}\)を基準として\({\dot E}_{\mathrm {f}}\)を求めると，①より，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {f}}&=&{\dot V}_{\mathrm {g}}+\mathrm {j}x_{\mathrm {g}}\dot I \\[ 5pt ] &=&{\dot V}_{\mathrm {g}}+\mathrm {j}x_{\mathrm {g}}\left( \frac {\overline {P_{\mathrm {g}}+\mathrm {j}Q_{\mathrm {g}}}}{\overline {{\dot V}_{\mathrm {g}}}}\right) \\[ 5pt ] &=&V_{\mathrm {g}}+\mathrm {j}x_{\mathrm {g}}\left( \frac {P_{\mathrm {g}}-\mathrm {j}Q_{\mathrm {g}}}{V_{\mathrm {g}}}\right) \\[ 5pt ] &=&\left(V_{\mathrm {g}}+\frac {Q_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) +\mathrm {j} \frac {P_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}}
\end{eqnarray}
\] となるので，発電機界磁電圧の大きさ\(E_{\mathrm {f}}\)は，
\[
E_{\mathrm {f}}=\sqrt {\left(V_{\mathrm {g}}+\frac {Q_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}+\left( \frac {P_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}}
\] と求められ，④と上式を比較すると，\(\displaystyle D=\frac {Q_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}}\)，\(\displaystyle F=\frac {P_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}}\)となる。

(2)\(x_{\mathrm {L}}=0.4\)，\(x_{\mathrm {g}}=1.8\)，\(V_{\mathrm {g}}=1.03\)，\(V_{\mathrm {i}}=0.83\)，\(P_{\mathrm {g}}=0.9\)のときの\(Q_{\mathrm {g}}\)及び\(E_{\mathrm {f}}\)
(1)より，
\[
\begin{eqnarray}
P_{\mathrm {g}}&=&\frac {V_{\mathrm {g}}V_{\mathrm {i}}}{x_{\mathrm {L}}}\sin \delta 　&・・・・・・⑦& \\[ 5pt ] Q_{\mathrm {g}}&=&\frac {V_{\mathrm {g}}}{x_{\mathrm {L}}}\left( V_{\mathrm {g}}-V_{\mathrm {i}}\cos \delta \right) 　&・・・・・・⑧& \\[ 5pt ] E_{\mathrm {f}}&=&\sqrt {\left(V_{\mathrm {g}}+\frac {Q_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}+\left( \frac {P_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}}　&・・・・・・⑨ &
\end{eqnarray}
\] である。⑦より，
\[
\begin{eqnarray}
\sin \delta &=&\frac {P_{\mathrm {g}}x_{\mathrm {L}}}{V_{\mathrm {g}}V_{\mathrm {i}}} \\[ 5pt ] &=&\frac {0.9\times 0.4}{1.03\times 0.83} \\[ 5pt ] &≒&0.42110
\end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\cos \delta&=&\sqrt {1-\sin ^{2}\delta } \\[ 5pt ] &=&\sqrt {1-0.42110 ^{2} } \\[ 5pt ] &≒&0.90701
\end{eqnarray}
\] となる。よって，⑧，⑨式に各値を代入して整理すると，
\[
\begin{eqnarray}
Q_{\mathrm {g}}&=&\frac {V_{\mathrm {g}}}{x_{\mathrm {L}}}\left( V_{\mathrm {g}}-V_{\mathrm {i}}\cos \delta \right) \\[ 5pt ] &=&\frac {1.03}{0.4}\left( 1.03-0.83\times 0.90701 \right) \\[ 5pt ] &≒&0.71374　→　0.714 [\mathrm {p.u.}] \\[ 5pt ] E_{\mathrm {f}}&=&\sqrt {\left(V_{\mathrm {g}}+\frac {Q_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}+\left( \frac {P_{\mathrm {g}}x_{\mathrm {g}}}{V_{\mathrm {g}}} \right) ^{2}} \\[ 5pt ] &=&\sqrt {\left(1.03+\frac {0.71374\times 1.8}{1.03} \right) ^{2}+\left( \frac {0.9\times 1.8}{1.03} \right) ^{2}} \\[ 5pt ] &≒&\sqrt {5.1862+2.4737} \\[ 5pt ] &≒&2.7677　→　2.77 [\mathrm {p.u.}]\\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)\(G\)，\(H\)，\(J\)を\(x_{\mathrm {g}}\)，\(x_{\mathrm {L}}\)，\(V_{\mathrm {i}}\)，\(P_{\mathrm {g}}\)，\(E_{\mathrm {f}}\)を用いて表す
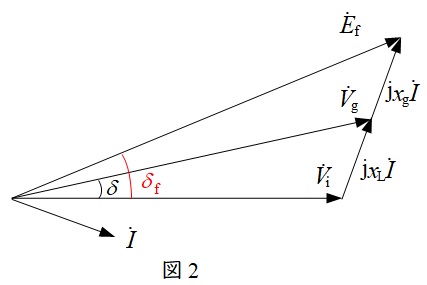
題意に沿って，ベクトル図を描くと図2のように修正される。図2より，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {f}}&=&{\dot V}_{\mathrm {i}}+\mathrm {j}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) \dot I \\[ 5pt ] \dot I&=&\frac {{\dot E}_{\mathrm {f}}-{\dot V}_{\mathrm {i}}}{\mathrm {j}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) }
\end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {g}}&=&{\dot E}_{\mathrm {f}}-\mathrm {j}x_{\mathrm {g}} \dot I \\[ 5pt ] &=&{\dot E}_{\mathrm {f}}-\mathrm {j}x_{\mathrm {g}} \frac {{\dot E}_{\mathrm {f}}-{\dot V}_{\mathrm {i}}}{\mathrm {j}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) } \\[ 5pt ] &=&{\dot E}_{\mathrm {f}}-\frac {x_{\mathrm {g}}}{x_{\mathrm {L}}+x_{\mathrm {g}}} \left( {\dot E}_{\mathrm {f}}-{\dot V}_{\mathrm {i}}\right) \\[ 5pt ] &=&\frac {x_{\mathrm {L}}}{x_{\mathrm {L}}+x_{\mathrm {g}}} {\dot E}_{\mathrm {f}}+\frac {x_{\mathrm {g}}}{x_{\mathrm {L}}+x_{\mathrm {g}}}{\dot V}_{\mathrm {i}}
\end{eqnarray}
\] となる。\({\dot V}_{\mathrm {i}}\)を基準にすると，\({\dot E}_{\mathrm {f}}=E_{\mathrm {f}}e^{\mathrm {j}\delta _{f}}=E_{\mathrm {f}}\left( \cos \delta _{\mathrm {f}}+\mathrm {j}\sin \delta _{\mathrm {f}}\right) \)で表されるので上式を整理すると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {g}}&=&\frac {x_{\mathrm {L}}}{x_{\mathrm {L}}+x_{\mathrm {g}}} {\dot E}_{\mathrm {f}}+\frac {x_{\mathrm {g}}}{x_{\mathrm {L}}+x_{\mathrm {g}}}{\dot V}_{\mathrm {i}} \\[ 5pt ] &=&\frac {x_{\mathrm {L}}}{x_{\mathrm {L}}+x_{\mathrm {g}}} E_{\mathrm {f}}\left( \cos \delta _{\mathrm {f}}+\mathrm {j}\sin \delta _{\mathrm {f}}\right)+\frac {x_{\mathrm {g}}}{x_{\mathrm {L}}+x_{\mathrm {g}}}V_{\mathrm {i}} \\[ 5pt ] &=&\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}\left( E_{\mathrm {f}} x_{\mathrm {L}} \cos \delta _{\mathrm {f}} + V_{\mathrm {i}}x_{\mathrm {g}} \right) +\mathrm {j}\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}E_{\mathrm {f}} x_{\mathrm {L}} \sin \delta _{\mathrm {f}}
\end{eqnarray}
\] となる。よって，発電機端子電圧の大きさ\(V_{\mathrm {g}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {g}}&=&\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}\sqrt {\left( E_{\mathrm {f}} x_{\mathrm {L}} \cos \delta _{\mathrm {f}} + V_{\mathrm {i}}x_{\mathrm {g}} \right) ^{2}+\left( E_{\mathrm {f}} x_{\mathrm {L}} \sin \delta _{\mathrm {f}} \right) ^{2}} \\[ 5pt ] &=&\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}\sqrt {\left( E_{\mathrm {f}} x_{\mathrm {L}}\right) ^{2} + \left( V_{\mathrm {i}}x_{\mathrm {g}}\right) ^{2} +2E_{\mathrm {f}} V_{\mathrm {i}}x_{\mathrm {L}}x_{\mathrm {g}} \cos \delta _{\mathrm {f}} } \\[ 5pt ] \end{eqnarray}
\] と求められ，⑤と上式を比較すると，\(G=\left( E_{\mathrm {f}} x_{\mathrm {L}}\right) ^{2} + \left( V_{\mathrm {i}}x_{\mathrm {g}}\right) ^{2} \)，\(H=2E_{\mathrm {f}} V_{\mathrm {i}}x_{\mathrm {L}}x_{\mathrm {g}}\)となる。
また\(P_{\mathrm {g}}\)は，
\[
P_{\mathrm {g}}=\frac {E_{\mathrm {f}}V_{\mathrm {i}}}{x_{\mathrm {L}}+x_{\mathrm {g}}}\sin \delta_{\mathrm {f}}
\] となるので，
\[
\begin{eqnarray}
\cos \delta_{\mathrm {f}}&=&\sqrt {1-\sin ^{2} \delta_{\mathrm {f}}} \\[ 5pt ] &=&\sqrt {1-\left[ \frac {P_{\mathrm {g}}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) }{E_{\mathrm {f}}V_{\mathrm {i}}}\right] ^{2} }
\end{eqnarray}
\] と求められ，⑥と上式を比較すると，\(\displaystyle J=\frac {P_{\mathrm {g}}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) }{E_{\mathrm {f}}V_{\mathrm {i}}}\)となる。

(4)\(x_{\mathrm {L}}=0.4\)，\(x_{\mathrm {g}}=1.8\)，\(V_{\mathrm {i}}=0.83\)，\(P_{\mathrm {g}}=0.9\)の条件で，界磁電圧の大きさ\(E_{\mathrm {f}}\)が\(2.45 \ \mathrm {p.u.}\)に制限された場合の，\(Q_{\mathrm {g}}\)及び\(V_{\mathrm {g}}\)
(3)の解答式に各値を代入すると，
\[
\begin{eqnarray}
\cos \delta_{\mathrm {f}}&=&\sqrt {1-\left[ \frac {P_{\mathrm {g}}\left( x_{\mathrm {L}}+x_{\mathrm {g}}\right) }{E_{\mathrm {f}}V_{\mathrm {i}}}\right] ^{2} } \\[ 5pt ] &=&\sqrt {1-\left[ \frac {0.9\times \left( 0.4+1.8\right) }{2.45\times 0.83}\right] ^{2} } \\[ 5pt ] &≒&0.22788
\end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
V_{\mathrm {g}}&=&\frac {1}{x_{\mathrm {L}}+x_{\mathrm {g}}}\sqrt {\left( E_{\mathrm {f}} x_{\mathrm {L}}\right) ^{2} + \left( V_{\mathrm {i}}x_{\mathrm {g}}\right) ^{2} +2E_{\mathrm {f}} V_{\mathrm {i}}x_{\mathrm {L}}x_{\mathrm {g}} \cos \delta _{\mathrm {f}} } \\[ 5pt ] &=&\frac {1}{0.4+1.8}\sqrt {\left( 2.45 \times 0.4\right) ^{2} + \left( 0.83 \times 1.8\right) ^{2} +2\times 2.45 \times 0.83 \times 0.4 \times 1.8 \times 0.22788 } \\[ 5pt ] &≒&\frac {1}{2.2}\sqrt {0.9604 + 2.2320 +0.66729 } \\[ 5pt ] &≒&0.89300　→　0.893 [\mathrm {p.u.}] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
\cos \delta&=&\sqrt {1-\left( \frac {P_{\mathrm {g}}x_{\mathrm {L}}}{V_{\mathrm {g}}V_{\mathrm {i}}} \right) ^{2}} \\[ 5pt ] &=&\sqrt {1-\left( \frac {0.9\times 0.4}{0.89300 \times 0.83} \right) ^{2}} \\[ 5pt ] &≒&0.87412
\end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
Q_{\mathrm {g}}&=&\frac {V_{\mathrm {g}}}{x_{\mathrm {L}}}\left( V_{\mathrm {g}}-V_{\mathrm {i}}\cos \delta \right) \\[ 5pt ] &=&\frac {0.89300}{0.4}\left( 0.89300-0.83\times 0.87412 \right) \\[ 5pt ] &≒&0.37390　→　0.374 [\mathrm {p.u.}] \end{eqnarray}
\] と求められる。