《機械・制御》〈回転機〉[R01:問1] 三相かご形誘導電動機の拘束試験に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

\( \ 180 \ \mathrm {kW} \ \)，\( \ 3000 \ \mathrm {V} \ \)，\( \ 6 \ \)極，\( \ 50 \ \mathrm {Hz} \ \)の定格をもつ三相かご形誘導電動機の拘束試験の結果は次のとおりであった。

線間電圧\( \ 610 \ \mathrm {V} \ \)，線電流\( \ 31 \ \mathrm {A} \ \)，三相入力\( \ 5.2 \ \mathrm {kW} \ \)

また，電機子巻線の接続は\( \ \mathrm {Y} \ \)接続とし，端子間の抵抗の平均値は\( \ 0.92 \ \mathrm {\Omega } \ \)であった。次の問に答えよ。ただし，励磁電流は無視する。

(1)　拘束試験時の二次入力\( \ \mathrm {[kW]} \ \)を求めよ。

(2)　定格電圧での拘束時の二次入力\( \ \mathrm {[kW]} \ \)を求めよ。

(3)　定格電圧始動時の始動トルク\( \ \mathrm {[N\cdot m]} \ \)を求めよ。

(4)　この電動機を定格電圧で始動した場合，始動トルクは全負荷トルクの\( \ 50.5 \ \mathrm {％} \ \)，始動電流は全負荷電流の\( \ 410 \ \mathrm {％} \ \)である。始動電流を全負荷電流の\( \ 200 \ \mathrm {％} \ \)に抑えるための始動電圧及びトルクを求めよ。ただし，全負荷運転時の滑りは\( \ 3 \ \mathrm {％} \ \)とする。

【ワンポイント解説】

拘束試験は誘導電動機の回転子を回転しないように拘束し，定格より低い電圧を加えて，一次電流がほぼ定格値になった時の入力電力，電圧，電流を測定する試験です。一次電圧が定格よりかなり小さいので，鉄損を無視し，滑りが\( \ 1 \ \)となることがポイントとなります。

1.三相誘導電動機の\( \ \mathrm {L} \ \)形等価回路
三相誘導電動機の一相あたりの\( \ \mathrm {L} \ \)形等価回路は図1のようになります。\( \ \mathrm {L} \ \)形等価回路は確実に描けるようにしておきましょう。

\[
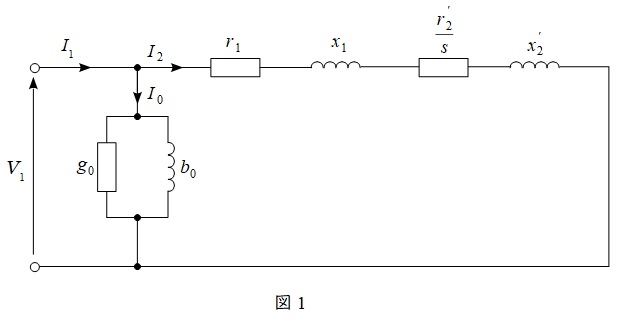
\begin{eqnarray}
V_{1}&：&一次電圧 \\[ 5pt ] I_{1}&：&一次電流 \\[ 5pt ] I_{0}&：&励磁電流 \\[ 5pt ] I^{\prime}_{2}&：&一次側に換算した二次電流 \\[ 5pt ] r_{1}&：&一次抵抗 \\[ 5pt ] x_{1}&：&一次リアクタンス \\[ 5pt ] r_{2}^{\prime}&：&一次側に換算した二次抵抗 \\[ 5pt ] x_{2}^{\prime}&：&一次側に換算した二次リアクタンス \\[ 5pt ] g_{0}&：&励磁コンダクタンス \\[ 5pt ] b_{0}&：&励磁サセプタンス \\[ 5pt ] s&：&滑り
\end{eqnarray}
\]

2.電動機の同期速度\( \ N_{\mathrm {s}} \ \)と同期角速度\( \ \omega _{\mathrm {s}} \ \)
周波数を\( \ f \ \)，極数\( \ p \ \)とすると，同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。また，同期角速度\( \ \omega _{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}}&=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\times \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

3.電動機のトルク\( \ T \ \)と出力\( \ P_{\mathrm {o}} \ \)の関係
電動機の出力\( \ P_{\mathrm {o}} \ \)は，電動機の角速度\( \ \omega \ \)，トルク\( \ T \ \)とすると，
\[
\begin{eqnarray}
P_{\mathrm {o}}&=&\omega T \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)拘束試験時の二次入力\( \ \mathrm {[kW]} \ \)
端子間の抵抗は\( \ 2 \ \)相分の抵抗なので，\( \ 1 \ \)相分の抵抗は，
\[
\begin{eqnarray}
r_{1}&=&\frac {0.92}{2} \\[ 5pt ] &=&0.46 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] である。拘束試験では\( \ s=1 \ \)であるので，三相入力は\( \ r_{1} \ \)と\( \ r_{2}^{\prime} \ \)で消費される。よって，拘束試験時の線電流\( \ I_{\mathrm {s}}=31 \ \mathrm {[A]} \ \)より，
\[
\begin{eqnarray}
r_{1}+r_{2}^{\prime}&=&\frac {5200}{3\times 31^{2}} \\[ 5pt ] &≒&1.8037 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，二次抵抗\( \ r_{2}^{\prime} \ \)は，
\[
\begin{eqnarray}
r_{2}^{\prime}&=&1.8037-0.46 \\[ 5pt ] &≒&1.3437 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，拘束試験時の二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3r_{2}^{\prime} I_{\mathrm {s}}^{2}\\[ 5pt ] &=&3\times 1.3437 \times 31^{2}\\[ 5pt ] &≒&3873.9 \ \mathrm {[W]}　→　3.87 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)定格電圧での拘束時の二次入力\( \ \mathrm {[kW]} \ \)
図1より拘束時すなわち\( \ s=1 \ \)の時のインピーダンスは変わらないので，電圧と電流は比例する。したがって，定格電圧時の線電流\( \ I_{\mathrm {s}}^{\prime} \ \)は，拘束試験時の線間電圧\( \ V_{\mathrm {s}}=610 \ \mathrm {[V]} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {s}}^{\prime}&=&\frac {V_{\mathrm {n}}}{V_{\mathrm {s}}}I_{\mathrm {s}}\\[ 5pt ] &=&\frac {3000}{610}\times 31 \\[ 5pt ] &≒&152.46 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，二次入力\( \ P_{2}^{\prime} \ \)は，
\[
\begin{eqnarray}
P_{2}^{\prime}&=&3r_{2}^{\prime} {I_{\mathrm {s}}^{\prime}}^{2}\\[ 5pt ] &=&3\times 1.3437 \times 152.46^{2}\\[ 5pt ] &≒&93699 \ \mathrm {[W]}　→　93.7 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)定格電圧始動時の始動トルク\( \ \mathrm {[N\cdot m]} \ \)
始動時回転数が\( \ 0 \ \)なので，始動時の滑り\( \ s \ \)は\( \ 1 \ \)である。したがって，拘束試験時のトルクと同様に計算すれば良い。電動機の同期角速度\( \ \omega _{\mathrm {s}} \ \)は，ワンポイント解説「2.電動機の同期速度\( \ N_{\mathrm {s}} \ \)と同期角速度\( \ \omega _{\mathrm {s}} \ \)」より，
\[
\begin{eqnarray}
\omega _{\mathrm {s}}&=&\frac {4\pi f}{p} \\[ 5pt ] &=&\frac {4\pi \times 50}{6} \\[ 5pt ] &≒&104.72 \ \mathrm {[rad/s]} \\[ 5pt ] \end{eqnarray}
\] であるので，定格電圧始動時の始動トルク\( \ T_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
T _{\mathrm {s}}&=&\frac {P_{2}^{\prime}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=&\frac {93699}{104.72} \\[ 5pt ] &≒&894.75　→　895 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)始動電流を全負荷電流の\( \ 200 \ \mathrm {％} \ \)に抑えるための始動電圧及びトルク
電圧と電流は比例し，トルクは二次入力に比例し，二次入力は二次電流の\( \ 2 \ \)乗に比例する。すなわち，電圧は電流に比例，トルクは電流の\( \ 2 \ \)乗に比例する。したがって，全負荷トルク\( \ T_{\mathrm {n}} \ \)及び全負荷電流\( \ I_{\mathrm {n}} \ \)と置くと，求める始動電圧\( \ V_{\mathrm {sx}} \ \)及び始動トルク\( \ T_{\mathrm {sx}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {sx}}&=&\frac {2I_{\mathrm {n}}}{I_{\mathrm {s}}^{\prime}}V_{\mathrm {n}} \\[ 5pt ] &=&\frac {2I_{\mathrm {n}}}{4.1I_{\mathrm {n}}}V_{\mathrm {n}} \\[ 5pt ] &=&\frac {2}{4.1}V_{\mathrm {n}} \\[ 5pt ] &=&\frac {2}{4.1}\times 3000 \\[ 5pt ] &≒&1463.4　→　1460 \ \mathrm {[V]} \\[ 5pt ] T_{\mathrm {sx}}&=&\frac {\left( 2I_{\mathrm {n}}\right) ^{2}}{{I_{\mathrm {s}}^{\prime}}^{2}}T_{\mathrm {s}} \\[ 5pt ] &=&\frac {2^{2}I_{\mathrm {n}}^{2}}{\left( 4.1I_{\mathrm {n}}\right) ^{2}}\cdot T _{\mathrm {s}} \\[ 5pt ] &=&\frac {2^{2}}{4.1^{2}}\cdot T _{\mathrm {s}} \\[ 5pt ] &=&\frac {2^{2}}{4.1^{2}}\times 894.75 \\[ 5pt ] &≒&212.91　→　212 \ \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。